个人模板

杂项

快读&O2优化

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#define inf1 0x3f3f3f3f
#define inf2 0x3f3f3f3f3f3f3f3f
const double Pi = acos(-1);
std::ios::sync_with_stdio(false);
std::cin.tie(0);
cout<<fixed<<setprecision(20)<<ans<<endl;

read函数快读

inline int read()
{
    int z = 0, flag = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            flag = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
    {
        z = z * 10 + ch - '0';
        ch = getchar();
    }
    return z * flag;
}

函数式__int128 输入和输出

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
__int128 int128read()
{
    __int128 x=0;
    int flag=1;
    string a;
    cin>>a;
    for(char c:a)
    {
        if(c=='-')
            flag=-1;
        else
            x=x*10+c-'0';
    }
    return flag*x;
}
void int128print(__int128 x)
{
    if(x<0)
    {
        putchar('-');
        x=-x;
    }
    if(x>9)
        int128print(x/10);
    putchar(x % 10 + '0');
}
int main()
{
    __int128 a=int128read(),b=int128read();
    int128print(a+b);
}

重载式 __int128 输入和输出

#include <bits/stdc++.h>
using namespace std;

istream &operator>>(istream &in, __int128 &x)
{
    x = 0;
    int flag = 1;
    string a;
    in >> a;
    for (char c : a)
    {
        if (c == '-')
            flag = -1;
        else
            x = x * 10 + c - '0';
    }
    x = flag * x;
    return in;
}

ostream &operator<<(ostream &out, __int128 &x)
{
    if (x < 0)
    {
        out << '-';
        x = -x;
    }
    stack<int> s;
    while (x)
    {
        s.push(x % 10);
        x /= 10;
    }
    while (!s.empty())
    {
        out << s.top();
        s.pop();
    }
    return out;
}

int main()
{
    __int128 a, b;
    cin >> a >> b;
    cout << a << ' ' << b << endl;
    return 0;
}

java ACM 基础

import java.io.*;
import java.math.*;
import java.util.*;

public class Main {
    public static void main(String args[])
    {
        //BigDecimal大数Double类
        //读入
        Scanner cin = new Scanner (new BufferedInputStream(System.in));
        int a; double b; BigInteger c; String d;
        a = cin.nextInt(); b = cin.nextDouble(); c = cin.nextBigInteger(); 
        d = cin.nextLine(); // 每种类型都有相应的输入函数.
        System.out.printf("输入的为%d %f %s %s\n",a,b,c.toString(),d);

        c=cin.nextBigInteger(2); //大数以2进制读入
        String tmp=c.toString(2); ///将大数以二进制形式输出

        System.out.print(1); // cout << …;
        System.out.println(1); // cout << … << endl;
        System.out.printf("%d",1); // 与C中的printf用法类似.

        ///字符串处理
        String st = "abcdefg";
        System.out.println(st.charAt(0)); // st.charAt(i)就相当于st[i].
        char [] ch;
        ch = st.toCharArray(); // 字符串转换为字符数组.
        for (int i = 0; i < ch.length; i++) ch[i] += 1;
        System.out.println(ch); // 输入为“bcdefgh”.
        if (st.startsWith("a")) // 如果字符串以'0'开头.
            st = st.substring(1); // 则从第1位开始copy(开头为第0位).

        ///进制转化
        int num=15,base=2;
        System.out.printf("15转2进制为%s\n",Integer.toString(num, base));
        st="1111";
        System.out.printf("2进制的1111转10进制为%d\n",Integer.parseInt(st, base)); 

        // 把st当做base进制，转成10进制的int(parseInt有两个参数,第一个为要转的字符串,第二个为进制). 
        BigInteger m = new BigInteger(st, base); // st是字符串，base是st的进制.

        ///排序
        int n=cin.nextInt();
        Integer[] arr=new Integer[n];
        for(int i=0;i<n;i++)
            arr[i]=cin.nextInt();

        Arrays.sort(arr,new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2-o1;            ///从大到小排序
            }
        });

        for(int i=0;i<n;i++)
            System.out.printf("%d ",arr[i]);
        System.out.println();

        ///清空
        Arrays.fill(arr,5);
        for(int i=0;i<n;i++)
            System.out.printf("%d ",arr[i]);
        System.out.println();

        ///二分查找
        System.out.println(Arrays.binarySearch(arr, 5));
        ///如果key在数组中，则返回搜索值的索引；否则返回-1或者”-“(插入点)。
        ///插入点是索引键将要插入数组的那一点，即第一个大于该键的元素索引。
    }
}

java BigInteger 运算

import java.io.*;
import java.math.*;
import java.util.*;

public class Main {

    public static void main(String args[]) 
    {
        Scanner cin = new Scanner(System.in);
        while (cin.hasNext()) ///相当于 scanf()!=EOF
        { 
            BigInteger a, b, c;

            //大数初始化
            //1.二进制字符串
            BigInteger interNum1 = new BigInteger("1011100111",2);
            //2.十进制字符串
            BigInteger interNum2 = new BigInteger("123456");
            //3.十进制数字
            BigInteger interNum3 = BigInteger.valueOf(8);

            //大数读入
            a = cin.nextBigInteger();
            b = cin.nextBigInteger();

            //基本运算
            //1.把a与b相加并赋给c
            c = a.add(b); 
            //2.把a与b相减并赋给c
            c = a.subtract(b); 
            //3.把a与b相乘并赋给c
            c = a.multiply(b); 
            //4.把a与b相除并赋给c
            c = a.divide(b);
            //5.取模，(需 b > 0，否则出现异常：ArithmeticException("BigInteger: modulus not positive"))
            c = a.mod(b);
            //6.求余
            c = a.remainder(b);
            //7.相当于a^b
            c = a.pow(2); 
            //8.根据该数值是小于、等于、或大于a 返回 -1、0 或 1
            int ans1 = a.compareTo(b);
            //9.判断两数是否相等，也可以用compareTo来代替
            boolean ans2 = a.equals(b); 
            //10.最大值和最小值
            c = a.min(b);
            c = a.max(b);

            //类型转换
            //1.转换为bigNum的二进制补码形式
            byte[] num1 = a.toByteArray(); 
            //2.转换为bigNum的十进制字符串形式
            String num2 = a.toString();    
            //3.转换为bigNum的radix进制字符串形式
            String num3 = a.toString(2);
            //4.将bigNum转换为int
            int num4 = a.intValue();
            //5.将bigNum转换为long
            long num5 = a.longValue();
            //6.将bigNum转换为float
            float num6 = a.floatValue();
            //7.将bigNum转换为double
            double num7 = a.doubleValue();

            //二进制运算
            //1.与：a&b
            BigInteger bigNum1 = a.and(b);
            //2.或：a|b
            BigInteger bigNum2 = a.or(b);
            //3.异或：a^b
            BigInteger bigNum3 = a.xor(b);
            //4.取反：~a
            BigInteger bigNum4 = a.not();
            //5.左移n位： (a << n)
            BigInteger bigNum5 = a.shiftLeft(3);
            //6.右移n位： (a >> n)
            BigInteger bigNum6 = a.shiftRight(3);
        }
    }
}

java BigDecimal 运算

import java.io.*;
import java.math.*;
import java.util.*;

public class Main {

    public static void main(String args[]) 
    {
        Scanner cin = new Scanner(System.in);
        while (cin.hasNext()) ///相当于 scanf()!=EOF
        { 
            BigDecimal a, b, c;

            //大数初始化
            //1.十进制字符串
            BigDecimal interNum1 = new BigDecimal("0.005");
            //2.十进制数字
            BigDecimal interNum2 =new BigDecimal(0.000005);
            BigDecimal interNum3 = BigDecimal.valueOf(0.000005);

            //大数读入
            a = cin.nextBigDecimal();
            b = cin.nextBigDecimal();

            //大数保留小数位输出
            BigDecimal d=a.setScale(10, RoundingMode.HALF_UP);//保留十位小数
            System.out.println(d);

            //基本运算
            //1.把a与b相加并赋给c
            c = a.add(b); 
            //2.把a与b相减并赋给c
            c = a.subtract(b); 
            //3.把a与b相乘并赋给c
            c = a.multiply(b); 
            //4.把a与b相除并赋给c
            c = a.divide(b,10,BigDecimal.ROUND_UP); //舍入远离零的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_DOWN); //接近零的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_CEILING); //接近正无穷大的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_FLOOR); //接近负无穷大的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_HALF_UP); //向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为向上舍入的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_HALF_DOWN); //向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则为上舍入的舍入模式。
            c = a.divide(b,10,BigDecimal.ROUND_HALF_EVEN); //向“最接近的”数字舍入，如果与两个相邻数字的距离相等，则向相邻的偶数舍入。
            //5.求余
            c = a.remainder(b);
            //6.相当于a^b
            c = a.pow(2); 
            //7.根据该数值是小于、等于、或大于a 返回 -1、0 或 1
            int ans1 = a.compareTo(b);
            //8.判断两数是否相等，也可以用compareTo来代替
            boolean ans2 = a.equals(b); 
            //9.最大值和最小值
            c = a.min(b);
            c = a.max(b);
            //10.绝对值
            c = a.abs();

            //类型转换
            //1.转换为bigNum的十进制字符串形式
            String num2 = a.toString();
            //2.将bigNum转换为int
            int num4 = a.intValue();
            //3.将bigNum转换为long
            long num5 = a.longValue();
            //4.将bigNum转换为float
            float num6 = a.floatValue();
            //5.将bigNum转换为double
            double num7 = a.doubleValue();
        }
    }
}

判断周几

int getWeek(int y, int m, int d) {
    if (m == 1 || m == 2) { 
        m += 12;     
        y--; 
    } 
    int week = (d +1 + 2 * m + 3 * (m + 1) / 5 + y + y / 4 - y / 100 + y / 400) % 7;
    return week;
}

组合数奇偶判断

图论

堆优化prim算法

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
struct node
{
    int to, val;
};
vector<node> v[100500];
struct node1
{
    int now, val;
    bool operator<(const node1 &a) const
    {
        return a.val < val;
    }
};
priority_queue<node1> que;
int dis[100500] = {0};
void prim()
{
    memset(dis, -1, sizeof(dis));
    que.push({1, 0});
    while (!que.empty())
    {
        node1 now = que.top();
        que.pop();
        if (dis[now.now] != -1)
            continue;
        dis[now.now] = now.val;
        for (int i = 0; i < v[now.now].size(); i++)
        {
            int to = v[now.now][i].to;
            int val = v[now.now][i].val;
            if (dis[to] != -1)
                continue;
            que.push({to, val});
        }
    }
}
int main()
{
    int n, m, from, to, val;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &from, &to, &val);
        v[from].push_back({to, val});
        v[to].push_back({from, val});
    }
    prim();
    ll ans = 0;
    for (ll i = 1; i <= n; i++)
    {
        if (dis[i] == -1)
            return 0 * puts("orz"); ///不连通
        ans += dis[i];
    }
    cout << ans << endl;
}

SPFA判断负环

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
#include <algorithm>
#define INF 0x3f3f3f3f

using namespace std;
const int MAXN = 5500;
int n,m,w;

struct Edge
{
    int v,w,next;
}edge[MAXN];
int head[MAXN],dis[MAXN],vis[MAXN],t;

void Init()
{
    memset(head,-1,sizeof(head));
    t = 0;
}
void Add_edge(int u,int v,int w)
{
    edge[t].v = v;edge[t].w = w;edge[t].next = head[u];head[u] = t++;
}

bool SPFA()
{
    int mark[MAXN];//记录每个点如队列的次数
    for(int i = 1;i <= n;i ++)
    {
        mark[i] = 0;dis[i] = INF;vis[i] = 0;
    }
    queue<int> q;
    q.push(1);  //我们只需要判断负环，随便找一个起点就好
    dis[1] = 0;
    vis[1] = 1;//入队列
    mark[1] ++;
    while(!q.empty())
    {
        int  u = q.front();
        q.pop();
        vis[u] = 0;//出队列
        for(int i = head[u];i != -1;i = edge[i].next)
        {
            int v = edge[i].v;
            if(dis[v] > dis[u] + edge[i].w)
            {
                dis[v] = dis[u] + edge[i].w;
                if(!vis[v])//不在队列中的时候出队
                {
                    q.push(v);mark[v] ++;vis[v] = 1;
                }
                if(mark[v] >= n)//如果不存在负环，那么最多更新n-1次就可以得到最终的答案，因为一次最少更新一个节点，那么如果出现了更新n次，那么就一定出现了负环
                    return false;
            }
        }
    }
    return true;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        Init();
        int u,v,z;
        scanf("%d%d%d",&n,&m,&w);
        for(int i = 0;i < m;i ++)
        {
            scanf("%d%d%d",&u,&v,&z);
            Add_edge(u,v,z);
            Add_edge(v,u,z);
        }
        for(int i = 0;i < w;i ++)
        {
            scanf("%d%d%d",&u,&v,&z);
            Add_edge(u,v,-z);
        }
        if(!SPFA())
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}

dijikastra第k短路

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAX = 1005;
int n,m;
int start,end,k;
struct Edge
{
    int w;
    int to;
    int next;
};
Edge e[100005];
int head[MAX],edgeNum;
int dis[MAX];   //dis[i]表示从i点到end的最短距离
bool vis[MAX];
int cnt[MAX];
vector<Edge> opp_Graph[MAX];

struct Node
{
    int f,g;    //f = g+dis[v]
    int v;      //当前到达的节点
    Node(int a, int b,int c):f(a),g(b),v(c){}
    bool operator < (const Node& a) const
    {
        return a.f < f;
    }
};

void addEdge(int from, int to, int w)
{
    e[edgeNum].to = to;
    e[edgeNum].w = w;
    e[edgeNum].next = head[from];
    head[from] = edgeNum++;
}

void dijikastra(int start)
{
    int i;
    memset(vis,0,sizeof(vis));
    for(i = 1; i <= n; i++)
        dis[i] = INF;
    dis[start] = 0;
    priority_queue<Node> que;
    que.push(Node(0,0,start));
    Node next(0,0,0);
    while(!que.empty())
    {
        Node now = que.top();
        que.pop();
        if(vis[now.v])              //从集合T中选取具有最短距离的节点
            continue;
        vis[now.v] = true;          //标记节点已从集合T加入到集合S中
        for(i = 0; i < opp_Graph[now.v].size(); i++)    //更新从源点到其它节点(集合T中)的最短距离
        {
            Edge edge = opp_Graph[now.v][i];
            if(!vis[edge.to] && dis[now.v] + edge.w < dis[edge.to])     //加不加前面的判断无所谓
            {
                dis[edge.to] = dis[now.v] + edge.w;
                next.f = dis[edge.to];
                next.v = edge.to;
                que.push(next);
            }
        }
    }
}

int A_Star()
{
    int i;
    priority_queue<Node> que;
    if(dis[start] == INF)
        return -1;
    que.push(Node(dis[start],0,start));
    Node next(0,0,0);
    while(!que.empty())
    {
        Node now = que.top();
        que.pop();
        cnt[now.v]++;
        if(cnt[end] == k)
            return now.f;
        if(cnt[now.v] > k)
            continue;
        for(i = head[now.v]; i != -1; i = e[i].next)
        {
            next.v = e[i].to;
            next.g = now.g + e[i].w;
            next.f = next.g + dis[e[i].to];
            que.push(next);
        }
    }
    return -1;
}

int main()
{
    int i;
    int from,to,w;
    edgeNum = 0;
    memset(head,-1,sizeof(head));
    memset(opp_Graph,0,sizeof(opp_Graph));
    memset(cnt,0,sizeof(cnt));
    scanf("%d %d",&n,&m);
    Edge edge;
    for(i = 1; i <= m; i++)
    {
        scanf("%d %d %d",&from,&to,&w);
        addEdge(from,to,w);
        edge.to = from;
        edge.w = w;
        opp_Graph[to].push_back(edge);
    }
    scanf("%d %d %d",&start,&end,&k);
    if(start == end)
        k++;
    dijikastra(end);
    int result = A_Star();
    printf("%d\n",result);
    return 0;
}

LCA+ST倍增算法

#include <bits/stdc++.h>
using namespace std;
//lca板子题,求俩个点最短距离
//树上两点最短路径:从根节点出发dis[u]+dis[v]-dis[lca]*2
struct node
{
    int to, next;
};
int tot = 0;
node edge[1000500] = {0};
int head[500500] = {0};
int fa[500500][18] = {0};
int dep[500500] = {0};
void add(int from, int to)
{
    edge[++tot].next = head[from];
    edge[tot].to = to;
    head[from] = tot;
}
void dfs(int now, int fa1)
{
    dep[now] = dep[fa1] + 1;
    fa[now][0] = fa1;
    for (int i = head[now]; i; i = edge[i].next)
    {
        int to = edge[i].to;
        if (to != fa1)
            dfs(to, now);
    }
}
int lca(int x, int y)
{
    if (dep[x] < dep[y])
        swap(x, y);
    for (int j = 17; j >= 0; j--)
    {
        if (dep[fa[x][j]] >= dep[y])
            x = fa[x][j];
    }
    if (x == y)
        return x;
    for (int j = 17; j >= 0; j--)
    {
        if (fa[x][j] != fa[y][j])
            x = fa[x][j], y = fa[y][j];
    }
    return fa[x][0];
}
int main()
{
    int n, m, s, f, t;
    scanf("%d%d%d", &n, &m, &s); ///s为根节点
    for (int i = 1; i <= n - 1; i++)
    {
        scanf("%d%d", &f, &t);
        add(f, t);
        add(t, f);
    }
    dfs(s, 0);
    for (int j = 1; j <= 17; j++)
    {
        for (int i = 1; i <= n; i++)
        {
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
        }
    }
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d", &f, &t);
        printf("%d\n", lca(f, t));
    }
}

树的直径

#include <bits/stdc++.h>

using namespace std;
struct node
{
    int to,val,next;
};
node edge[200500]={0};
int head[200500]={0};
int cnt=0;
int add_edge(int from,int to,int val)
{
    edge[++cnt].next=head[from];
    edge[cnt].to=to;
    edge[cnt].val=val;
    head[from]=cnt;
}
int dp[200500][4]={0};
int down[200500]={0};
int up[200500]={0};
int len[200500][3]={0};
int dfs1(int now,int fa)
{
    for(int i=head[now];i;i=edge[i].next)
    {
        int to=edge[i].to,val=edge[i].val;
        if(to==fa)
            continue;
        dfs1(to,now);
        int tmp=dp[to][0]+val;
        if(tmp>dp[now][0])swap(dp[now][0],tmp);
        if(tmp>dp[now][1])swap(dp[now][1],tmp);
        if(tmp>dp[now][2])swap(dp[now][2],tmp);
        down[now]=max(down[now],down[to]);
    }
    down[now]=max(down[now],dp[now][0]+dp[now][1]);
}
int dfs2(int now,int fa)
{
    for(int i=head[now];i;i=edge[i].next)
    {
        if(edge[i].to==fa)
            continue;
        int tem=down[edge[i].to];
        if(tem>len[now][0])
            swap(tem,len[now][0]);
        if(tem>len[now][1])
            swap(tem,len[now][1]);
    }
    for(int i=head[now];i;i=edge[i].next)
    {
        int to=edge[i].to,val=edge[i].val;
        if(to==fa)
            continue;
        if(dp[now][0]==dp[to][0]+val)
        {
            dp[to][3]=max(dp[now][1],dp[now][3])+val;
            up[to]=max(dp[now][2],dp[now][3])+dp[now][1];
        }
        else if(dp[now][1]==dp[to][0]+val)
        {
            dp[to][3]=max(dp[now][0],dp[now][3])+val;
            up[to]=max(dp[now][2],dp[now][3])+dp[now][0];
        }
        else
        {
            dp[to][3]=max(dp[now][0],dp[now][3])+val;
            up[to]=max(dp[now][1],dp[now][3])+dp[now][0];
        }
        if(len[now][0]==down[to])
            up[to]=max(up[to],len[now][1]);
        else
            up[to]=max(up[to],len[now][0]);
        dfs2(to,now);
    }
}
int main()
{
    int n,from,to,val;
    scanf("%d",&n);
    for(int i=1;i<=n-1;i++)
    {
        scanf("%d%d%d",&from,&to,&val);
        add_edge(from,to,val);
        add_edge(to,from,val);
    }
    dfs1(1,-1);
    dfs2(1,-1);
    int ans=0;
    for(int i=1;i<=n;i++)
        ans=max(ans,up[i]+down[i]);
    cout<<ans<<endl;
}

最大流算法

EK算法：

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
struct node
{
    ll to,val,next;
};
node edge[805]={0};
ll head[205]={0};
ll cnt=0;
ll s=1,e=1;
void add_edge(ll from,ll to,ll val)
{
    edge[cnt].next=head[from];
    edge[cnt].to=to;
    edge[cnt].val=val;
    head[from]=cnt++;
}
ll pre[205]={0},tag[205]={0},vis[205]={0};
ll bfs()
{
    queue<ll>que;
    memset(tag,0,sizeof(tag));
    memset(pre,0,sizeof(pre));
    memset(vis,0,sizeof(vis));
    que.push(s);
    vis[s]=1;
    while(!que.empty())
    {
        ll now=que.front();
        que.pop();
        for(ll i=head[now];i!=-1;i=edge[i].next)
        {
            ll to=edge[i].to,val=edge[i].val;
            if(!vis[to]&&val>0)
            {
                vis[to]=1;
                pre[to]=now;
                tag[to]=i;
                if(to==e)
                    return 1;
                que.push(to);
            }
        }
    }
    return 0;
}
ll EK()
{
    ll ans=0;
    while(bfs())
    {
        ll min1=inf;
        for(ll i=e;i!=s;i=pre[i])
        {
            min1=min(min1,edge[tag[i]].val);
        }
        for(ll i=e;i!=s;i=pre[i])
        {
            edge[tag[i]].val-=min1;
            edge[tag[i]^1].val+=min1;
        }
        ans+=min1;
    }
    return ans;
}
int main()
{
    ll n,m,from,to,val;
    while(scanf("%lld%lld",&m,&n) == 2&&n){
        e=n;
        cnt=0;
        for(int i=1;i<=n;i++)
            head[i]=-1;
        for(ll i=1;i<=m;i++)
        {
            scanf("%lld%lld%lld",&from,&to,&val);
            add_edge(from,to,val);
            add_edge(to,from,0);
        }
        printf("%lld\n",EK());
    }
}

优化版Dinic算法：

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;

struct Edge
{
    ll from, to, cap, flow, index;
    Edge(ll from, ll to, ll cap, ll flow, ll index) : from(from), to(to), cap(cap), flow(flow), index(index) {}
};

struct Dinic
{
    ll N;
    vector<vector<Edge>> G;
    vector<Edge *> dad;
    vector<ll> Q;
    Dinic(ll N) : N(N), G(N), dad(N), Q(N) {}
    void AddEdge(ll from, ll to, ll cap)
    {
        G[from].push_back(Edge(from, to, cap, 0, G[to].size()));
        if (from == to)
            G[from].back().index++;
        G[to].push_back(Edge(to, from, 0, 0, G[from].size() - 1));
    }
    ll BlockingFlow(ll s, ll t)
    {
        fill(dad.begin(), dad.end(), (Edge *)NULL);
        dad[s] = &G[0][0] - 1;

        ll head = 0, tail = 0;
        Q[tail++] = s;
        while (head < tail)
        {
            ll x = Q[head++];
            for (ll i = 0; i < G[x].size(); i++)
            {
                Edge &e = G[x][i];
                if (!dad[e.to] && e.cap - e.flow > 0)
                {
                    dad[e.to] = &G[x][i];
                    Q[tail++] = e.to;
                }
            }
        }
        if (!dad[t])
            return 0;
        ll totflow = 0;
        for (ll i = 0; i < G[t].size(); i++)
        {
            Edge *start = &G[G[t][i].to][G[t][i].index];
            ll amt = INF;
            for (Edge *e = start; amt && e != dad[s]; e = dad[e->from])
            {
                if (!e)
                {
                    amt = 0;
                    break;
                }
                amt = min(amt, e->cap - e->flow);
            }
            if (amt == 0)
                continue;
            for (Edge *e = start; amt && e != dad[s]; e = dad[e->from])
            {
                e->flow += amt;
                G[e->to][e->index].flow -= amt;
            }
            totflow += amt;
        }
        return totflow;
    }

    ll GetMaxFlow(ll s, ll t)
    {
        ll totflow = 0;
        while (ll flow = BlockingFlow(s, t))
            totflow += flow;
        return totflow;
    }
};

int main()
{
    ll n, m, f, t, v, s, e;
    scanf("%lld%lld", &n, &m);
    scanf("%lld%lld", &s, &e);
    Dinic dinic(n + 10);
    for (ll i = 1; i <= m; i++)
    {
        scanf("%lld%lld%lld", &f, &t, &v);
        dinic.AddEdge(f, t, v);
    }
    printf("%lld\n", dinic.GetMaxFlow(s, e));
}

普通版本dinic：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF = 1e18;
const int N = 5e2 + 7;
const int M = 2e5 + 7;

int head[N], nex[M], ver[M], tot = 1;
ll edge[M];
int n, m, s, t;
ll maxflow;
ll deep[N]; //层级数，其实应该是level
int now[M]; //当前弧优化
queue<int> q;

inline void add(int x, int y, int z)
{ //建正边和反向边
    ver[++tot] = y;
    edge[tot] = z;
    nex[tot] = head[x];
    head[x] = tot;
    ver[++tot] = x;
    edge[tot] = 0;
    nex[tot] = head[y];
    head[y] = tot;
}

inline bool bfs()
{ //在残量网络中构造分层图
    for (int i = 1; i <= n; i++)
        deep[i] = INF;
    while (!q.empty())
        q.pop();
    q.push(s);
    deep[s] = 0;
    now[s] = head[s]; //一些初始化
    while (!q.empty())
    {
        int x = q.front();
        q.pop();
        for (int i = head[x]; i; i = nex[i])
        {
            int y = ver[i];
            if (edge[i] > 0 && deep[y] == INF)
            { //没走过且剩余容量大于0
                q.push(y);
                now[y] = head[y]; //先初始化，暂时都一样
                deep[y] = deep[x] + 1;
                if (y == t)
                    return 1; //找到了
            }
        }
    }
    return 0;
}

//flow是整条增广路对最大流的贡献，rest是当前最小剩余容量，用rest去更新flow
ll dfs(int x, ll flow)
{ //在当前分层图上增广
    if (x == t)
        return flow;
    ll ans = 0, k, i;
    for (i = now[x]; i && flow; i = nex[i])
    {
        now[x] = i; //当前弧优化（避免重复遍历从x出发的不可拓展的边）
        int y = ver[i];
        if (edge[i] > 0 && (deep[y] == deep[x] + 1))
        {                                   //必须是下一层并且剩余容量大于0
            k = dfs(y, min(flow, edge[i])); //取最小
            if (!k)
                deep[y] = INF; //剪枝，去掉增广完毕的点
            edge[i] -= k;      //回溯时更新
            edge[i ^ 1] += k;  //成对变换
            ans += k;
            flow -= k;
        }
    }

    return ans;
}

void dinic()
{
    while (bfs())
        maxflow += dfs(s, INF);
}

int main()
{
    scanf("%d%d%d%d", &n, &m, &s, &t);
    tot = 1;
    for (ll i = 1; i <= m; i++)
    {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        add(x, y, z);
    }
    dinic();
    printf("%lld\n", maxflow);
    return 0;
}

最小费用最大流算法

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
struct node
{
    int next;
    int flow;
    int dis;
    int to;
};
int head[100500]= {0};
node edge[100500]= {0};
int dis[100500]= {0};
int pre[100500]= {0};
int vis[100500]= {0};
int last[100500]= {0};
int flow[100500]={0};
char g[1000][1000]= {0};
int n,m,s,t,cnt=-1,maxflow=0,mincost=0;
int num(int i,int j)
{
    return i*m+j;
}
int add(int from,int to,int flow,int dis)
{
    edge[++cnt].next=head[from];
    edge[cnt].to=to;
    edge[cnt].flow=flow;
    edge[cnt].dis=dis;
    head[from]=cnt;
}
queue<int>w;
bool spfa(int start,int end1)
{
    w.push(start);
    memset(dis,0x3f3f3f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    memset(flow,0x3f3f3f,sizeof(flow));
    pre[end1]=-1;
    vis[start]=1;
    dis[start]=0;
    while(!w.empty())
    {
        int now=w.front();
        w.pop();
        vis[now]=0;
        for(int i=head[now]; i!=-1; i=edge[i].next)
        {
            //cout<<i<<endl;
            if(edge[i].flow>0&&dis[edge[i].to]>dis[now]+edge[i].dis)
            {
                dis[edge[i].to]=dis[now]+edge[i].dis;
                pre[edge[i].to]=now;
                last[edge[i].to]=i;
                flow[edge[i].to]=min(flow[now],edge[i].flow);
                if(!vis[edge[i].to])
                {
                    vis[edge[i].to]=1;
                    w.push(edge[i].to);
                }
            }
        }
    }
    return pre[end1]!=-1;
}
int MCMF()
{
    while(spfa(s,t))
    {
        maxflow+=flow[t];
        mincost+=dis[t]*flow[t];
        int now=t;
        while(now!=s)
        {
            edge[last[now]].flow-=flow[t];
            edge[last[now]^1].flow+=flow[t];
            now=pre[now];
        }
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    s=n*m+200,t=n*m+100;
    for(int i=1; i<=n; i++)
    {
        scanf("%s",g[i]+1);
    }
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=m; j++)
        {
            if(g[i][j]=='x')
                continue;
            if(j>1&&g[i][j-1]!='x')
            {
                add(num(i,j),num(i,j-1),1,1);
                add(num(i,j-1),num(i,j),0,-1);
            }
            if(i>1&&g[i-1][j]!='x')
            {
                add(num(i,j),num(i-1,j),1,1);
                add(num(i-1,j),num(i,j),0,-1);
            }
            if(j<m&&g[i][j+1]!='x')
            {
                add(num(i,j),num(i,j+1),1,1);
                add(num(i,j+1),num(i,j),0,-1);
            }
            if(i<n&&g[i+1][j]!='x')
            {
                add(num(i,j),num(i+1,j),1,1);
                add(num(i+1,j),num(i,j),0,-1);
            }
            if(g[i][j]=='F')
            {
                add(s,num(i,j),2,0);
                add(num(i,j),s,0,0);
            }
            if(g[i][j]=='C'||g[i][j]=='B')
            {
                add(num(i,j),t,1,0);
                add(t,num(i,j),0,0);
            }
        }
    }
    MCMF();
   // cout<<maxflow<<" "<<mincost<<endl;
    if(maxflow!=2)
        printf("-1\n");
    else
        printf("%d\n",mincost);
}

二分图模板

题意：给你n个长度相同，包含字母种类相同，每种字母数量相同，让你确定一个字符串集合，集合中的任意一个串不能通过交换任意两个不同的位置变成集合中的另一个串，问你集合最大有多个字符串。

思路：

我们对于两个一次操作（交换两个不同位置）不能互相变换的串建边，那么答案就是这个图的最大团。 一个图的最大团等于这个图补图的最大独立集，那么我们要建这个图的补图。 这个图的补图就是对能够一次操作互相变换的两个串建边。 那么现在答案就是这个补图的最大独立集。 这个补图一定是一个二分图。 二分图的最大独立集等于图中点的个数 - 最大匹配数。 所以我们现在可以对这个二分图求一个最大匹配。

#include <bits/stdc++.h>

using namespace std;
char a[1000][300] = {0};
int mp[1000][1000] = {0};
map<int, int> mp1, vis;
int n;
int dfs(int k)
{
    for (int i = 1; i <= n; i++)
    {
        if (mp[i][k] &&!vis[i])
        {
            vis[i] = 1;
            if (mp1[i] == 0 || dfs(mp1[i]))
            {
                mp1[i] = k;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    scanf("%d", &n);  ///两个字符串中不能有两个字符相同，问至少需要分为多少组
    for (int i = 1; i <= n; i++)
        scanf("%s", a[i] + 1);
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            int sum = 0;
            for (int k = 1; a[i][k]; k++)
            {
                if (a[i][k] != a[j][k])
                    sum++;
            }
            if (sum == 2)
                mp[i][j] = 1;
        }
    }
    //cout<<mp[1][2]<<endl;
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        vis.clear();
        ans += dfs(i);
    }
    cout << n - ans / 2 << endl;
}

二分图判断

#include <bits/stdc++.h>
using namespace std;
vector<int> v[100500];
int color[100500] = {0};
int bfs(int i)
{
    queue<int> que;
    que.push(i);
    while (!que.empty())
    {
        int now = que.front();
        que.pop();
        for (int i : v[now])
        {
            if (color[i] == 0)
            {
                color[i] = 3 - color[now];
                que.push(i);
            }
            else
            {
                if (color[i] == color[now])
                    return 0;
            }
        }
    }
    return 1;
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
    {
        int from, to;
        scanf("%d %d", &from, &to);
        v[from].push_back(to);
        v[to].push_back(from);
    }
    for (int i = 1; i <= m; i++)
    {
        if (color[i] == 0)
        {
            int tmp = bfs(i);
            if (tmp == 0)
            {
                puts("No");
                return 0;
            }
        }
    }
    puts("Yes");
}
/*
输入：
7 6
1 2
1 3
2 4
2 5
3 6
3 7
输出：
Yes
输入：
3 3
1 2
2 3
1 3
输出：
No
*/

二分图最大匹配

#include <bits/stdc++.h>
using namespace std;
vector<int> v[100500];
map<int, int> mp, vis, mp1;
int dfs(int now)
{
    for (int i = 0; i < v[now].size(); i++)
    {
        int to = v[now][i];
        if (!vis[to])
        {
            vis[to] = 1;
            if (mp[to] == 0 || dfs(mp[to]))
            {
                mp[to] = now;
                mp1[now] = to;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int n1, n2, m;
    scanf("%d%d%d", &n1, &n2, &m);
    int from, to;
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d", &from, &to);
        to += n1;
        v[from].push_back(to);
        v[to].push_back(from);
    }
    int ans = 0;
    for (int i = 1; i <= n1; i++)
    {
        vis.clear();
        ans += dfs(i);
    }
    cout << ans << endl;
    for (int i = 1; i <= n1; i++)
        cout << max(0,mp1[i]-n1) << ' ';
}

二分图最大独立集：

选最多的点，满足两两之间没有边相连。

二分图中，最大独立集 =n- 最大匹配。

二分图最小点覆盖：

选最少的点，满足每条边至少有一个端点被选，不难发现补集是独立集。

二分图中，最小点覆盖 =n- 最大独立集。

二分图有向无向建图规则：

有左右之分建单向边，无左右之分建无向边 答案除2

一切树均为二分图

二分图最大权匹配：

题目：https://uoj.ac/problem/80

题解：https://blog.csdn.net/weixin_30528371/article/details/99263983

讲解：https://www.cnblogs.com/wenruo/p/5264235.html

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
int n, m, q;
int w[405] = {0}, v[405] = {0};
int vl[405] = {0}, vr[405] = {0}, c[405] = {0};
int a[405][405] = {0}, ans[405] = {0}, b[405] = {0};
int tim = 0;
int dfs(int x)
{
    vl[x] = tim;
    for (int i = 1; i <= m; i++)
    {
        if (vr[i] == tim)
            continue;
        int d = w[x] + v[i] - a[x][i];
        if (d == 0)
        {
            vr[i] = tim;
            if (!b[i] || dfs(b[i]))
            {
                b[i] = x;
                return 1;
            }
        }
        else
        {
            c[i] = min(c[i], d);
        }
    }
    return 0;
}
void km()
{
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            w[i] = max(w[i], a[i][j]);
    for (int i = 1; i <= n; i++)
    {
        memset(c, inf, sizeof(c));
        tim += 1;
        if (dfs(i))
            continue;

        while (1)
        {
            int d = inf, y = 0;
            for (int j = 1; j <= m; j++)
                if (vr[j] != tim)
                    d = min(d, c[j]);

            for (int j = 1; j <= n; j++)
                if (vl[j] == tim)
                    w[j] -= d;

            for (int j = 1; j <= m; j++)
            {
                if (vr[j] == tim)
                    v[j] += d;
                else if (!(c[j] -= d))
                    y = j;
            }

            if (!b[y])
                break;

            int x = b[y];
            vl[x] = vr[y] = tim;
            for (int j = 1; j <= m; j++)
                c[j] = min(c[j], w[x] + v[j] - a[x][j]);
        }
        tim += 1;
        dfs(i);
    }
    ll ans1 = 0;
    for (int i = 1; i <= m; i++)
        ans1 += a[b[i]][i];
    printf("%lld\n", ans1);
    for (int i = 1; i <= m; i++)
    {
        if (a[b[i]][i])
            ans[b[i]] = i;
    }
    for (int i = 1; i <= n; i++)
        printf("%d ", ans[i]);
}
int main()
{
    scanf("%d%d%d", &n, &m, &q);
    m = max(m, n);
    for (int i = 1; i <= q; i++)
    {
        int x, y, v;
        scanf("%d%d%d", &x, &y, &v);
        a[x][y] = v;
    }
    km();
}

Tarjan算法

Tarjan 算法及其应用

1. 求割边

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
struct node
{
    int to, next;
};
node edge[200500] = {0};
int head[200500] = {0}, dfn[200500] = {0}, low[200500] = {0}, bridge[200500] = {0};
int cnt = 1, tot = 0;
void add_edge(int from, int to)
{
    edge[++cnt] = {to, head[from]};
    head[from] = cnt;
}
void tarjan(int x, int in_edge)
{
    dfn[x] = low[x] = ++tot;
    for (int i = head[x]; i; i = edge[i].next)
    {
        int y = edge[i].to;
        if (!dfn[y])
        {
            tarjan(y, i);
            low[x] = min(low[x], low[y]);
            if (low[y] > dfn[x])
                bridge[i] = bridge[i ^ 1] = 1; ///桥
        }
        else if (i != (in_edge ^ 1))
            low[x] = min(low[x], dfn[y]);
    }
}
int main()
{
    int n, m, from, to;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; i++)
    {
        scanf("%d%d", &from, &to);
        add_edge(from, to);
        add_edge(to, from);
    }
    for (int i = 1; i <= n; i++)
    {
        if (!dfn[i])
            tarjan(i, 0);
    }
    for (int i = 2; i <= cnt; i += 2)
    {
        if (bridge[i])
        {
            printf("%d %d\n", edge[i ^ 1].to, edge[i].to);
        }
    }
}

1. 缩点求将图转变为强连通图需要加边的数目

题目来源：POJ 2767

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
struct node
{
    int to, next;
};
node edge[200500] = {0};
int head[200500] = {0}, dfn[200500] = {0}, low[200500] = {0};
int stack1[200500] = {0}, vis[200500] = {0}, color[200500] = {0};
bool in[200500] = {0}, out[200500] = {0};
int cnt = 0, tot = 0, top = 0, color_num = 0;
void add_edge(int from, int to)
{
    edge[++cnt] = {to, head[from]};
    head[from] = cnt;
}
void tarjan(int now)
{
    stack1[++top] = now;
    vis[now] = 1;
    dfn[now] = low[now] = ++tot;
    for (int i = head[now]; i; i = edge[i].next)
    {
        int y = edge[i].to;
        if (!dfn[y])
        {
            tarjan(y);
            low[now] = min(low[now], low[y]);
        }
        else if (vis[y])
            low[now] = min(low[now], dfn[y]);
    }
    if (dfn[now] == low[now]) ///强连通块
    {
        color[now] = ++color_num;
        vis[now] = 0;
        while (stack1[top] != now)
        {
            color[stack1[top]] = color_num;
            vis[stack1[top--]] = 0;
        }
        vis[stack1[top]] = 0;
        top--;
    }
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        int n, m, from, to;
        scanf("%d%d", &n, &m);
        for (int i = 0; i <= n + 1; i++)
            in[i] = out[i] = head[i] = dfn[i] = low[i] = stack1[i] = vis[i] = color[i] = 0;
        cnt = 0, tot = 0, top = 0, color_num = 0;
        for (int i = 1; i <= m; i++)
        {
            scanf("%d%d", &from, &to);
            add_edge(from, to);
        }
        for (int i = 1; i <= n; i++)
        {
            if (!dfn[i])
                tarjan(i);
        }
        if (color_num == 1)
        {
            printf("0\n");
            continue;
        }
        int in_num = color_num, out_num = color_num;
        for (int i = 1; i <= n; i++)
        {
            for (int j = head[i]; j; j = edge[j].next)
            {
                int to = edge[j].to;
                if (color[to] != color[i])
                {
                    if (!in[color[to]])
                    {
                        in_num--;
                        in[color[to]] = 1;
                    }
                    if (!out[color[i]])
                    {
                        out_num--;
                        out[color[i]] = 1;
                    }
                }
            }
        }
        printf("%d\n", max(out_num, in_num));
    }
}

1. 求割点

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
struct node
{
    int to, next;
};
node edge[200500] = {0};
int head[200500] = {0}, dfn[200500] = {0}, low[200500] = {0}, cut[200500] = {0};
int cnt = 0, tot = 0;
void add_edge(int from, int to)
{
    edge[++cnt] = {to, head[from]};
    head[from] = cnt;
}
void tarjan(int now, int root)
{
    dfn[now] = low[now] = ++tot;
    int ct = 0;
    for (int i = head[now]; i; i = edge[i].next)
    {
        int y = edge[i].to;
        ct++;
        if (!dfn[y])
        {
            tarjan(y, root);
            low[now] = min(low[now], low[y]);
            if (now != root && low[y] >= dfn[now])
                cut[now] = 1;
            if (now == root && ct > 1)
                cut[now] = 1;
        }
        else
            low[now] = min(low[now], dfn[y]);
    }
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        int n, m, from, to;
        scanf("%d%d", &n, &m);
        for (int i = 0; i <= n + 1; i++)
            head[i] = dfn[i] = low[i] = cut[i] = 0;
        cnt = 0, tot = 0;
        for (int i = 1; i <= m; i++)
        {
            scanf("%d%d", &from, &to);
            add_edge(from, to);
            add_edge(to, from);
        }
        for (int i = 1; i <= n; i++)
        {
            if (!dfn[i])
                tarjan(i, i);
        }
        for (int i = 1; i <= n; i++)
        {
            if (cut[i])
                printf("%d ", i);
        }
        printf("\n");
    }
}
/*
输入：
1
7 7
1 2
1 5
5 6
5 7
2 3
2 4
3 4
割点为：
1 2 5 
*/

树链剖分+线段树

https://oi-wiki.org/graph/hld/#_4

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll sum[400500] = {0}, lazy[400500] = {0};
ll dep[200500] = {0}, size1[200500] = {0}, son[200500] = {0}, f[200500] = {0}, id[200500] = {0}, top[200500] = {0};
struct node
{
    ll to, next;
};
node edge[400500] = {0};
ll head[400500] = {0};
ll num = 0, cnt = 0;
void add_edge(ll from, ll to)
{
    edge[++num] = {to, head[from]};
    head[from] = num;
}
void dfs1(ll now, ll fa)
{
    size1[now] = 1;
    for (ll i = head[now]; i; i = edge[i].next)
    {
        ll to = edge[i].to;
        if (to == fa)
            continue;
        f[to] = now;
        dep[to] = dep[now] + 1;
        dfs1(to, now);
        size1[now] += size1[to];
        if (size1[to] > size1[son[now]])
            son[now] = to;
    }
}
void dfs2(ll now, ll fa)
{
    id[now] = ++cnt;
    top[now] = fa;
    if (son[now])
        dfs2(son[now], fa);
    for (ll i = head[now]; i; i = edge[i].next)
    {
        ll to = edge[i].to;
        if (to == f[now] || to == son[now])
            continue;
        dfs2(to, to);
    }
}
void push_down(ll t, ll l, ll r)
{
    if (lazy[t] == 0)
        return;
    lazy[2 * t + 1] += lazy[t];
    lazy[2 * t] += lazy[t];
    ll mid = (l + r) / 2;
    sum[2 * t] += (mid - l + 1) * lazy[t];
    sum[2 * t + 1] += (r - mid) * lazy[t];
    lazy[t] = 0;
}
void push_up(ll t)
{
    sum[t] = sum[2 * t] + sum[2 * t + 1];
}
void update(ll t, ll l, ll r, ll L, ll R, ll add)
{
    if (l <= L && R <= r)
    {
        lazy[t] += add;
        sum[t] += add * (R - L + 1);
        return;
    }
    push_down(t, L, R);
    ll mid = (L + R) / 2;
    if (l <= mid)
        update(2 * t, l, r, L, mid, add);
    if (mid < r)
        update(2 * t + 1, l, r, mid + 1, R, add);
    push_up(t);
}
ll query(ll t, ll l, ll r, ll L, ll R)
{
    if (l <= L && R <= r)
        return sum[t];
    push_down(t, L, R);
    ll mid = (L + R) / 2;
    ll ans = 0;
    if (l <= mid)
        ans += query(2 * t, l, r, L, mid);
    if (mid < r)
        ans += query(2 * t + 1, l, r, mid + 1, R);
    return ans;
}
void update_chain(ll x, ll y)
{
    ll fx = top[x], fy = top[y];
    while (fx != fy) ///不在同一条重链上
    {
        if (dep[fx] < dep[fy])
            swap(x, y), swap(fx, fy);
        update(1, id[fx], id[x], 1, cnt, 1);
        x = f[fx], fx = top[x]; ///跳转到另一条重链
    }
    if (id[x] > id[y])
        swap(x, y);
    update(1, id[x] + 1, id[y], 1, cnt, 1);
}
ll query_chain(ll x, ll y)
{
    ll fx = top[x], fy = top[y], ans = 0;
    while (fx != fy) ///不在同一条重链上
    {
        if (dep[fx] < dep[fy])
            swap(x, y), swap(fx, fy);
        ans += query(1, id[fx], id[x], 1, cnt);
        x = f[fx], fx = top[x]; ///跳转到另一条重链
    }
    if (id[x] > id[y])
        swap(x, y);
    ans += query(1, id[x] + 1, id[y], 1, cnt);
    return ans;
}
int main()
{
    ll n, m, from, to;
    scanf("%lld%lld", &n, &m);
    for (ll i = 1; i <= n - 1; i++)
    {
        scanf("%lld%lld", &from, &to);
        add_edge(from, to);
        add_edge(to, from);
    }
    f[1] = 0, dep[1] = 1;
    dfs1(1, 0), dfs2(1, 1);
    char c[10];
    for (ll i = 1; i <= m; i++)
    {
        scanf("%s%lld%lld", c + 1, &from, &to);
        if (c[1] == 'P')
            update_chain(from, to);
        else
            printf("%lld\n", query_chain(from, to));
    }
}

分层最短路

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
const int N = 100000 + 5;
const int K = 10 + 5;
const ll inf = 0x3f3f3f3f3f3f3f3f;

vector< pii > e[N];

struct Info {
    int pos, num;
    ll val;
    inline Info(){}
    inline Info(int _pos, int _num, ll _val) {
        pos = _pos, num = _num, val = _val;
    }
    inline bool operator < (const Info & b) const {
        return val > b.val;
    }
};

ll f[N][K];
bool vis[N][K];
priority_queue<Info> q;

class TaskL {
public:
    void solve(std::istream& in, std::ostream& out) {
        int T;
        in >> T;
        while (T--) {
            int n, m, k;
            in >> n >> m >> k;
            while (q.size()) q.pop();
            for (int i = 1; i <= n; ++i) {
                e[i].clear();
                for (int j = 0; j <= k; ++j) {
                    f[i][j] = inf;
                    vis[i][j] = false;
                }
            }
            for (int i = 1, x, y, z; i <= m; ++i) {
                in >> x >> y >> z;
                e[x].push_back({y, z});
            }
            f[1][0] = 0;
            q.push(Info(1, 0, 0));
            while (q.size()) {
                Info now = q.top(); q.pop();
                if (vis[now.pos][now.num] == true) continue;
                vis[now.pos][now.num] = true;
                for (int i = 0; i < e[now.pos].size(); ++i) {
                    int to = e[now.pos][i].first, val = e[now.pos][i].second;
                    if (f[to][now.num] > f[now.pos][now.num] + val) {
                        f[to][now.num] = f[now.pos][now.num] + val;
                        q.push(Info(to, now.num, f[to][now.num]));
                    }
                    if (now.num < k && f[to][now.num + 1] > f[now.pos][now.num]) {
                        f[to][now.num + 1] = f[now.pos][now.num];
                        q.push(Info(to, now.num + 1, f[to][now.num + 1]));
                    }
                }
            }
            ll ans = inf;
            for (int i = 0; i <= k; ++i) {
                ans = min(ans, f[n][i]);
            }
            out << ans << endl;
        }
    }
};


int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    TaskL solver;
    std::istream& in(std::cin);
    std::ostream& out(std::cout);
    solver.solve(in, out);
    return 0;
}

LCT 动态树

参考链接：

https://www.luogu.com.cn/problem/P3690

https://www.cnblogs.com/zwfymqz/p/7896036.html#!comments

https://www.cnblogs.com/zzy2005/p/10312977.html

https://www.cnblogs.com/JeremyGJY/p/5921594.html

https://blog.csdn.net/qq_36551189/article/details/79152612

#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[100500] = {0}, c[100500][2] = {0}, v[100500] = {0}, s[100500] = {0}, st[100500] = {0};
bool r[100500] = {0};
//判断节点是否为一个Splay的根
inline bool nroot(register ll x)
{
    return c[f[x]][0] == x || c[f[x]][1] == x;
    //原理为如果连的是轻边，他的父亲的儿子里没有它
}
//上传信息
inline void pushup(ll x)
{
    s[x] = s[c[x][0]] ^ s[c[x][1]] ^ v[x];
}
//翻转操作
inline void pushr(register ll x)
{
    register ll t = c[x][0];
    c[x][0] = c[x][1];
    c[x][1] = t;
    r[x] ^= 1;
}
//判断并释放懒标记
inline void pushdown(register ll x)
{
    if (r[x])
    {
        if (c[x][0])
            pushr(c[x][0]);
        if (c[x][1])
            pushr(c[x][1]);
        r[x] = 0;
    }
}
//一次旋转
inline void rotate(register ll x)
{
    register ll y = f[x], z = f[y], k = c[y][1] == x, w = c[x][!k];
    if (nroot(y))
        c[z][c[z][1] == y] = x;
    c[x][!k] = y;
    c[y][k] = w;
    if (w)
        f[w] = y;
    f[y] = x;
    f[x] = z;
    pushup(y);
}
//只传了一个参数，因为所有操作的目标都是该Splay的根
inline void splay(register ll x)
{
    register ll y = x, z = 0;
    st[++z] = y; //st为栈，暂存当前点到根的整条路径，pushdown时一定要从上往下放标记
    while (nroot(y))
        st[++z] = y = f[y];
    while (z)
        pushdown(st[z--]);
    while (nroot(x))
    {
        y = f[x];
        z = f[y];
        if (nroot(y))
            rotate((c[y][0] == x) ^ (c[z][0] == y) ? x : y);
        rotate(x);
    }
    pushup(x);
}
//访问
inline void access(register ll x)
{
    for (register ll y = 0; x; x = f[y = x])
        splay(x), c[x][1] = y, pushup(x);
}
//换根
inline void makeroot(register ll x)
{
    access(x);
    splay(x);
    pushr(x);
}
//找根（在真实的树中的）
inline ll findroot(register ll x)
{
    access(x);
    splay(x);
    while (c[x][0])
        pushdown(x), x = c[x][0];
    splay(x);
    return x;
}
//提取路径
inline void split(register ll x, register ll y)
{
    makeroot(x);
    access(y);
    splay(y);
}
//连边
inline void link(register ll x, register ll y)
{
    makeroot(x);
    if (findroot(y) != x)
        f[x] = y;
}
//断边
void cut(register ll x, register ll y)
{
    makeroot(x);
    if (findroot(y) == x && f[y] == x && !c[y][0])
    {
        f[y] = c[x][1] = 0;
        pushup(x);
    }
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) //给定 n 个点以及每个点的权值
        scanf("%d", &v[i]);
    for (int i = 1; i <= m; i++)
    {
        int opt, x, y;
        scanf("%d%d%d", &opt, &x, &y);
        if (opt == 0) //代表询问从 x 到 y 的路径上的点的权值的 xor 和。保证 x 到 y 是联通的。
        {
            split(x, y);
            printf("%d\n", s[y]);
        }
        else if (opt == 1) //代表连接 x 到 y，若 x 到 y 已经联通则无需连接。
        {
            link(x, y);
        }
        else if (opt == 2) //代表删除边 (x,y)，不保证边 (x,y) 存在。
        {
            cut(x, y);
        }
        else if (opt == 3) //代表将点 x 上的权值变成 y。
        {
            splay(x);
            v[x] = y;
        }
    }
}

数据结构

树状数组前缀和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
ll a[100500]={0};
ll c[100500]={0};
ll lowbit(ll x)
{
    return x&(-x);
}
ll update(ll k,ll x)
{
    for(ll i=k;i<=n;i+=lowbit(i))
        c[i]+=x;
}
ll sum1(ll k)
{
    ll ans=0;
    for(ll i=k;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;
}
int main()
{
    ll a1,b1,c1;
    scanf("%lld%lld",&n,&m);
    for(ll i=1;i<=m;i++)
    {
        scanf("%lld%lld%lld",&a1,&b1,&c1);
        if(a1==0)
            update(b1,c1);
        else
            printf("%lld\n",sum1(c1)-sum1(b1-1));
    }
}

线段树维护区间和

#include <stdio.h>
using namespace std;
typedef long long ll;
ll num[100500]={0};
ll lazy[800500]={0};
ll sum[800500]={0};
void push_up(ll t)
{
    sum[t]=sum[2*t]+sum[2*t+1];
}
void push_down(ll t,ll l,ll r)
{
    if(lazy[t]==0)
        return ;
    lazy[2*t]+=lazy[t];
    lazy[2*t+1]+=lazy[t];
    ll mid=(l+r)/2;
    sum[2*t]+=lazy[t]*(mid-l+1);
    sum[2*t+1]+=lazy[t]*(r-mid);
    lazy[t]=0;
}
void build(ll t,ll l,ll r)
{
    if(l==r)
    {
        sum[t]=num[l];
        return ;
    }
    ll mid=(l+r)/2;
    build(2*t,l,mid);
    build(2*t+1,mid+1,r);
    push_up(t);
}
void update(ll t,ll l,ll r,ll L,ll R,ll add) ///l,r为更新区间，L,R为线段树区间
{
    if(l<=L&&r>=R)
    {
        sum[t]+=add*(R-L+1);
        lazy[t]+=add;
        return ;
    }
    push_down(t,L,R);
    ll mid=(L+R)/2;
    if(l<=mid)
        update(2*t,l,r,L,mid,add);
    if(mid<r)
        update(2*t+1,l,r,mid+1,R,add);
    push_up(t);
}
ll query_sum(ll t,ll l,ll r,ll L,ll R) ///l,r为更新区间，L,R为线段树区间
{
    if(l<=L&&r>=R)
    {
        return sum[t];
    }
    push_down(t,L,R);
    ll mid=(L+R)/2,sum=0;
    if(l<=mid)
        sum+=query_sum(2*t,l,r,L,mid);
    if(mid<r)
        sum+=query_sum(2*t+1,l,r,mid+1,R);
    return sum;
}
int main()
{
    ll n,m;
    scanf("%lld%lld",&n,&m);
    for(ll i=1;i<=n;i++)
        scanf("%lld",&num[i]);
    build(1,1,n);
    char s[10];
    ll l,r,x;
    for(ll i=1;i<=m;i++)
    {
        scanf("%s%lld%lld",s,&l,&r);
        if(s[0]=='Q')
        {
            printf("%lld\n",query_sum(1,l,r,1,n));
        }
        else
        {
            scanf("%lld",&x);
            update(1,l,r,1,n,x);
        }
    }
}

划分树求中位数

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>

using namespace std;
int tree[20][100500]={0};
int to[20][100500]={0};
int num[100500]={0};
int sorted[100500]={0};
int build(int l,int r,int deep)
{
    if(l==r)
        return 0;
    int mid=(l+r)/2;
    int midd=sorted[mid];
    int suppose=mid-l+1;
    for(int i=l;i<=r;i++)
    {
        if(tree[deep][i]<midd)
            suppose--;
    }
    int sleft=l,sright=mid+1;
    for(int i=l;i<=r;i++)
    {
        if(i==l)
            to[deep][l]=0;
        else
            to[deep][i]=to[deep][i-1];
        if(tree[deep][i]<midd)
        {
            to[deep][i]++;
            tree[deep+1][sleft++]=tree[deep][i];
        }
        else if(tree[deep][i]==midd&&suppose>0)
        {
            suppose--;
            to[deep][i]++;
            tree[deep+1][sleft++]=tree[deep][i];
        }
        else
        {
            tree[deep+1][sright++]=tree[deep][i];
        }
    }
    build(l,mid,deep+1);
    build(mid+1,r,deep+1);
}
int query(int l,int r,int L,int R,int k,int deep)
{
    if(L==R)
        return tree[deep][L];
    int mid=(l+r)/2;
    int lef;
    int toleft;
    if(l==L)
        lef=0,toleft=to[deep][R];
    else
        lef=to[deep][L-1],toleft=to[deep][R]-lef;
    if(k<=toleft)
    {
        return query(l,mid,l+lef,l+toleft+lef-1,k,deep+1);
    }
    else
    {
        return query(mid+1,r,mid+L-l-lef+1,mid+R-l-toleft-lef+1,k-toleft,deep+1);
    }
}
int main()
{
    int n,m,summ=0;
    while(scanf("%d",&n)!=EOF)
    {
        summ++;
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&num[i]);
            sorted[i]=num[i];
            tree[0][i]=num[i];
        }
        sort(sorted+1,sorted+n+1);
        build(1,n,0);
        printf("Case %d:\n",summ);
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            int a,b,c; /// a,b,c代表查询a到b区间内第c大的数
            scanf("%d%d",&a,&b);
            c=(b-a)/2+1;
            printf("%d\n",query(1,n,a,b,c,0));
        }
    }
}

单调栈

单调栈 是在栈的**先进后出**基础之上额外添加一个特性：**从栈顶到栈底**的元素是严格递增或递减。

为了维护栈的单调性，在进栈过程中需要进行判断，具体进栈过程如下：假设当前进栈元素为 e，

• 对于单调递增栈，从栈顶开始遍历元素，把小于 e 或者等于 e 的元素弹出栈，直至遇见一个大于 e 的元素或者栈为空为止，然后再把 e 压入栈中，这样就能满足从栈顶到栈底的元素是递增的
• 对于单调递减栈，则每次弹出的是大于 e 或者等于 e 的元素，直至遇见一个小于e的元素或者栈为空为止

单调栈的作用在于

• 单调递增栈从栈顶到栈底是递增的，栈中保留的都是比当前入栈元素大的值，因此可以快速找到入栈元素左边比他大的元素
• 单调递减栈从栈顶到栈底是递减的，栈中保留的都是比当前入栈元素小的值，因此可以快速找到入栈元素左边比他小的元素

单调栈求区间长度和区间最小值乘积最大值：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node
{
    ll pos, val;
};
node s[2005000] = {0};
ll a[2005000] = {0};
int main()
{
    ll n, top = 0, ans = 0;
    scanf("%lld", &n);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &a[i]);
    for (int j = 1; j <= n + 1; j++)
    {
        if (top == 0)
        {
            s[++top] = {j, a[j]};
        }
        else
        {
            while (s[top].val > a[j]) ///递增栈
            {
                ll tmp = (j - s[top - 1].pos - 1) * s[top].val;
                ans = max(ans, tmp);
                top--;
            }
            s[++top] = {j, a[j]};
        }
    }
    printf("%lld\n", ans);
    return 0;
}

线性基

线性基求交，参考与：https://blog.csdn.net/qcwlmqy/article/details/97584411

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
using namespace std;
const int maxn=50500;
typedef long long ll;
class Bit_Set
{
public:
    ll d[32];
    Bit_Set()
    {
        memset(d,0,sizeof(d));
    }
    Bit_Set(const Bit_Set& t)
    {
        for(int i=0; i<=31; i++)
            d[i]=t.d[i];
    }
    void clear()
    {
        memset(d,0,sizeof(d));
    }
    void insert(ll x)
    {
        for(int i=31; i>=0; i--)
        {
            if(x&(ll(1)<<i))
            {
                if(!d[i])
                {
                    d[i]=x;
                    return ;
                }
                x^=d[i];
            }
        }
    }
    bool check(ll x)
    {
        for(int i=31; i>=0; i--)
        {
            if(x&(ll(1)<<i))
            {
                if(!d[i])
                    return false;
                x^=d[i];
            }
        }
        return true;
    }
    void show()
    {
        for(int i=0; i<=31; i++)
            cout<<i<<' '<<d[i]<<endl;
    }
    friend Bit_Set operator + (const Bit_Set& a, const Bit_Set& b)
    {
        Bit_Set a_b(a),c,res;
        for(int i=31; i>=0; i--)
        {
            if(b.d[i])
            {
                ll x=b.d[i],k=ll(1)<<i;
                bool flag=true;
                for(int j=31; j>=0; j--)
                {
                    if(x & (ll(1) << j))
                    {
                        if(a_b.d[j])
                        {
                            x^=a_b.d[j];
                            k^=c.d[j];   //将用上的b元素计入k
                        }
                        else
                        {
                            flag=false; //若不能被a_b表示，将b[i]加入数组
                            a_b.d[j]=x;
                            c.d[j]^=k;   //将a_b中b元素标记
                            break;
                        }
                    }
                }
                if(flag)
                {
                    ll x=0;
                    for(int j=31; j>=0; j--)
                    {
                        if(k&(ll(1)<<j))
                            x^=b.d[j];
                        //将用上的b元素和本身的b[i]异或在一起，
                        //由(a[argv---]^b[argv---]^b[i]==0),所得即为V1的贡献
                    }
                    res.insert(x);
                }
            }
        }
        return res;
    }
};
Bit_Set tree[maxn<<2];
void build(ll t,ll l,ll r)
{
    if(l==r)
    {
        int k;
        ll x;
        scanf("%d",&k);
        while(k--)
        {
            scanf("%lld",&x);
            tree[t].insert(x);
        }
        return ;
    }
    int mid=(l+r)/2;
    build(2*t,l,mid);
    build(2*t+1,mid+1,r);
    tree[t]=tree[2*t]+tree[2*t+1];
}
int query(ll t,ll l,ll r,ll L,ll R,ll x)
{
    if(l<=L&&R<=r)
    {
        return tree[t].check(x);
    }
    int flag=1;
    int mid=(L+R)/2;
    if(l<=mid)
        flag&=query(2*t,l,r,L,mid,x);
    if(r>mid)
        flag&=query(2*t+1,l,r,mid+1,R,x);
    return flag;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    build(1,1,n);
    while(m--)
    {
        int l,r,x;
        scanf("%d%d%d",&l,&r,&x);
        if(query(1,l,r,1,n,x))
            puts("YES");
        else
            puts("NO");
    }
}

线性基基础

性质

对于一个数组，存在一些数构成该数组的线性基

线性基有三大很优美的性质

• 数组中所有数均可以由线性基中部分数异或得到
• 数组中所有数异或出来均不为0
• 对于同一数组线性基个数唯一 例如$2 ，4 ， 5 ， 6 <span class="arithmatex"><span class="MathJax_Preview">,由线性基</span><script type="math/tex">,由线性基$1 , 2 , 4 1 , 2 , 4 $数组所有数均可以由$1,2,41,2,4异或得到

线性基构造

数组每加入一个数，对线性基进行修改 令线性基为d[32] ,数组长度为max(a[i])的最大二进制（所有数均可以由$ 1 , 2 , 4 ⋯ ,2^n$ 表示）

void add(int x) {
    for(int i=31; i>=0; i--) {  //i为线性基下标
        if(x&(1<<i)) { 
            if(d[i])x^=d[i];    //若该二进制位已有值，异或寻找线性基能否表达x^d[i]
            else {
                d[i]=x;         //若二进制位没有值，说明x不能被线性基表达，令d[i]=x
                break;          //记得如果插入成功一定要退出
            }
        }
    }
}

构造合理性：

• 若能插入x ，则将d[i] =x，x可以由线性基表达
• 若不能插入x，则x最终异或为0，即可以由线性基表达

区间异或最大值

数组$( L , R )$ 内取若干个数，使这些数异或后得到的值最大

令$d [ 32 ] <span class="arithmatex"><span class="MathJax_Preview">数组表示线性基的值，</span><script type="math/tex">数组表示线性基的值，$p [ 32 ]p [ 32 ]数组表示线性基的位置（为了便于询问，位置尽量存偏右的）

int ask(int l,int r){
    int res=0;
    for（int i=31;i>=0;i--）
        if(p[i]>=l&&(res^d[i])>res)
            res^=d[i];
    return res;
}

贪心：高位能变成1，就变成1（高位1比低位都变成1都有价值）

区间异或第k大

先将线性基处理成$ 1 , 2 , 4 , ⋯ ,2^n$ 的二进制表达形式

去除为0的异或值，每一位d[i] =1 相当于可以表达的二进制位数增加一位

void work() {           //将线性基转化为2进制
    for(int i=1; i<=31; i++)
        for(int j=1; j<=i; j++)
            if(d[i]&(1<<(j-1)))
                d[i]^=d[j-1];
}
int k_th(int k) {
    if(k==1&&tot<n)return 0;   //特判一下，假如k=1，并且原来的序列可以异或出0，就要返回0，
                               //tot表示线性基中的元素个数，n表示序列长度
    if(tot<n)k--;       //类似上面，去掉0的情况，因为线性基中只能异或出不为0的解
    work();
    int ans=0;
    for(int i=0; i<=31; i++)
        if(d[i]!=0) {
            if(k&1)ans^=d[i];
            k>>=1;
        }
}

主席树

参考链接：

https://blog.csdn.net/zuzhiang/article/details/78173412

https://www.cnblogs.com/s1124yy/p/6258026.html

https://blog.csdn.net/tianwei0822/article/details/79439054

主席树维护区间第k大数

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
int L[3200500] = {0}, R[3200500] = {0}, sum[3200500] = {0};
int tot = 0;
int a[3200500] = {0}, hash1[3200500] = {0}, T[3200500] = {0};
int build(int l, int r)
{
    int root = ++tot;
    sum[root] = 0;
    if (l < r)
    {
        int mid = (l + r) / 2;
        L[root] = build(l, mid);
        R[root] = build(mid + 1, r);
    }
    return root;
}
int update(int pre, int l, int r, int pos)
{
    int root = ++tot;
    L[root] = L[pre];
    R[root] = R[pre];
    sum[root] = sum[pre] + 1;
    if (l < r)
    {
        int mid = (l + r) / 2;
        if (pos <= mid)
            L[root] = update(L[pre], l, mid, pos);
        else
            R[root] = update(R[pre], mid + 1, r, pos);
    }
    return root;
}
int query(int l1, int r1, int l, int r, int k) //参数分别为：两颗线段树根节点的编号，左右端点，第k大
{
    if (l >= r)
        return l;
    int mid = (l + r) / 2;
    int num = sum[L[r1]] - sum[L[l1]];
    if (num >= k)
        return query(L[l1], L[r1], l, mid, k);
    else
        return query(R[l1], R[r1], mid + 1, r, k - num);
}
int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        tot = 0;
        int n, m;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]), hash1[i] = a[i];
        sort(hash1 + 1, hash1 + n + 1);
        int d = unique(hash1 + 1, hash1 + n + 1) - hash1 - 1;
        T[0] = build(1, d);
        for (int i = 1; i <= n; i++)
        {
            int pos = lower_bound(hash1 + 1, hash1 + d + 1, a[i]) - hash1;
            T[i] = update(T[i - 1], 1, d, pos);
        }
        for (int i = 1; i <= m; i++)
        {
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            int pos = query(T[l - 1], T[r], 1, d, k);
            printf("%d\n", hash1[pos]);
        }
    }
}

查询区间内小于等于给定的K的数的个数

题目链接：https://acm.hdu.edu.cn/showproblem.php?pid=4417

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
int L[3200500] = {0}, R[3200500] = {0}, sum[3200500] = {0};
int tot = 0;
int a[3200500] = {0}, hash1[3200500] = {0}, T[3200500] = {0};
int build(int l, int r)
{
    int root = ++tot;
    sum[root] = 0;
    if (l < r)
    {
        int mid = (l + r) / 2;
        L[root] = build(l, mid);
        R[root] = build(mid + 1, r);
    }
    return root;
}
int update(int pre, int l, int r, int pos)
{
    int root = ++tot;
    L[root] = L[pre];
    R[root] = R[pre];
    sum[root] = sum[pre] + 1;
    if (l < r)
    {
        int mid = (l + r) / 2;
        if (pos <= mid)
            L[root] = update(L[pre], l, mid, pos);
        else
            R[root] = update(R[pre], mid + 1, r, pos);
    }
    return root;
}
int query(int l1, int r1, int l, int r, int k)
{
    if (k < hash1[l])
        return 0;
    if (hash1[r] <= k)
        return sum[r1] - sum[l1];
    int mid = (l + r) / 2;
    if (k <= hash1[mid])
    {
        return query(L[l1], L[r1], l, mid, k);
    }
    else
    {
        int num = 0;
        num += sum[L[r1]] - sum[L[l1]];
        num += query(R[l1], R[r1], mid + 1, r, k);
        return num;
    }
}
int main()
{
    int t;
    scanf("%d", &t);
    for (int t1 = 1; t1 <= t; t1++)
    {
        tot = 0;
        int n, m;
        scanf("%d%d", &n, &m);
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]), hash1[i] = a[i];
        sort(hash1 + 1, hash1 + n + 1);
        int d = unique(hash1 + 1, hash1 + n + 1) - hash1 - 1;
        T[0] = build(1, d);
        for (int i = 1; i <= n; i++)
        {
            int pos = lower_bound(hash1 + 1, hash1 + d + 1, a[i]) - hash1;
            T[i] = update(T[i - 1], 1, d, pos);
        }
        printf("Case %d:\n", t1);
        for (int i = 1; i <= m; i++)
        {
            int l, r, k;
            scanf("%d%d%d", &l, &r, &k);
            int ans = query(T[l], T[r + 1], 1, d, k);
            printf("%d\n", ans);
        }
    }
}

ST表

ST 表是用于解决 可重复贡献问题 的数据结构。

可重复贡献问题 是指对于运算$opt$，满足$x\quad opt\quad x = x$ ，则对应的区间询问就是一个可重复贡献问题。例如，最大值有$max(x,x)=x$，gcd 有$gcd(x,x)=x$ ，所以 RMQ 和区间 GCD 就是一个可重复贡献问题。像区间和就不具有这个性质，如果求区间和的时候采用的预处理区间重叠了，则会导致重叠部分被计算两次，这是我们所不愿意看到的。另外， $opt$还必须满足结合律才能使用 ST 表求解。

一维ST表模板

#include <stdio.h>
#include <math.h>
#define max(a, b) (a > b ? a : b)
#define min(a, b) (a < b ? a : b)
using namespace std;
int a[50050] = {0}, dp_max[50050][30] = {0}, dp_min[50050][30] = {0};
int n, m;
void st()
{
    for (int i = 1; i <= n; i++)
        dp_max[i][0] = dp_min[i][0] = a[i];
    for (int j = 1; (1 << j) <= n; j++)
    {
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            dp_max[i][j] = max(dp_max[i][j - 1], dp_max[i + (1 << (j - 1))][j - 1]);
            dp_min[i][j] = min(dp_min[i][j - 1], dp_min[i + (1 << (j - 1))][j - 1]);
        }
    }
}
int query_max(int l, int r)
{
    int k = log2(r - l + 1);
    return max(dp_max[l][k], dp_max[r - (1 << k) + 1][k]);
}
int query_min(int l, int r)
{
    int k = log2(r - l + 1);
    return min(dp_min[l][k], dp_min[r - (1 << k) + 1][k]);
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    st();
    while (m--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query_max(l, r) - query_min(l, r));
    }
}

一维ST维护GCD模板

题目大意为给定长度为n的序列，后面又m次询问，询问满足区间gcd为给定数值的个数。

算法为二分+ST表，由于区间中不同GCD个数最多为log个，所以时间复杂度$nlog(n)$

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100500] = {0}, dp[100500][30] = {0};
map<ll, ll> mp;
ll n, m, k;
void st()
{
    for (ll i = 1; i <= n; i++)
        dp[i][0] = a[i];
    for (ll j = 1; (1 << j) <= n; j++)
    {
        for (ll i = 1; i + (1 << j) - 1 <= n; i++)
        {
            dp[i][j] = __gcd(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);
        }
    }
}
ll query(ll l, ll r)
{
    ll k = log2(r - l + 1);
    return __gcd(dp[l][k], dp[r - (1 << k) + 1][k]);
}
int main()
{
    scanf("%lld", &n);
    for (ll i = 1; i <= n; i++)
        scanf("%lld", &a[i]);
    st();
    for (ll i = 1; i <= n; i++)
    {
        ll cur = i, gc = a[i];
        while (cur <= n)
        {
            ll l = cur, r = n;
            while (l < r)
            {
                ll mid = (l + r + 1) / 2;
                if (query(cur, mid) == gc)
                    l = mid;
                else
                    r = mid - 1;
            }
            if (mp.count(gc) == 0)
                mp[gc] = (l - cur + 1);
            else
                mp[gc] += (l - cur + 1);
            cur = l + 1;
            if (cur <= n)
                gc = __gcd(gc, a[cur]);
        }
    }
    scanf("%lld", &m);
    for (ll i = 1; i <= m; i++)
    {
        scanf("%lld", &k);
        printf("%lld\n", mp[k]);
    }
    return 0;
}

二维ST表模板

#include <bits/stdc++.h>
using namespace std;
int dp_max[300][300][20] = {0};
int dp_min[300][300][30] = {0};
int a[300][300] = {0};
int n, m;
void st()
{
    for (int i = 1; i <= n; i++)
    {
        for (int k = 0; (1 << k) <= m; k++)
        {
            for (int j = 1; j + (1 << k) - 1 <= m; j++)
            {
                if (k == 0)
                    dp_max[i][j][k] = dp_min[i][j][k] = a[i][j];
                else
                {
                    dp_max[i][j][k] = max(dp_max[i][j][k - 1], dp_max[i][j + (1 << (k - 1))][k - 1]);
                    dp_min[i][j][k] = min(dp_min[i][j][k - 1], dp_min[i][j + (1 << (k - 1))][k - 1]);
                }
            }
        }
    }
}
int query_max(int x, int y, int xx, int yy)
{
    int k = log2(yy - y + 1);
    int mm = 0;
    for (int i = x; i <= xx; i++)
        mm = max(mm, max(dp_max[i][y][k], dp_max[i][yy - (1 << k) + 1][k]));
    return mm;
}
int query_min(int x, int y, int xx, int yy)
{
    int k = log2(yy - y + 1);
    int mm = 0x3f3f3f3f;
    for (int i = x; i <= xx; i++)
        mm = min(mm, min(dp_min[i][y][k], dp_min[i][yy - (1 << k) + 1][k]));
    return mm;
}
int main()
{
    int b, k;
    scanf("%d%d%d", &n, &b, &k);
    m = n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);
    st();
    while (k--)
    {
        int p, q;
        scanf("%d%d", &p, &q);
        int ans1 = query_max(p, q, p + b - 1, q + b - 1);
        int ans2 = query_min(p, q, p + b - 1, q + b - 1);
        printf("%d\n", ans1 - ans2);
    }
    return 0;
}

字符串

KMP算法

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const ll N = 1005000;
ll Next[N];
char s[N];
char t[N];
ll  tlen,len;
void getNext(char s[N])
{
    ll j=0,k=-1;
    Next[0]=-1;
    while(j<tlen)
    {
        if(k==-1||s[j]==s[k])
        {
            Next[++j]=++k;
        }
        else
            k=Next[k];
    }
}
int main()
{
    while(1)
    {
        scanf("%s",s);
        if(s[0]=='.')
        break;
        tlen=strlen(s);
        len=tlen;
        getNext(s);
        ll kk=tlen-Next[tlen];
        if(strlen(s)%kk==0)
        {
            printf("%d\n",strlen(s)/kk);
        }
        else
        { 
            printf("1\n");   //如果不能除尽，说明有后缀，例如abababa，这种情况只能为1
        }
    }
    return 0;
}

字符串哈希

给一个长度为n的字符串(1<=n<=200000),他只包含**小写**字母

找到这个字符串多少个前缀是M形字符串.

M形字符串定义如下:

他由两个相同的回文串拼接而来,第一个回文串的结尾字符和第二个字符串的开始字符可以重叠,也就是以下都是M 形字符串.

abccbaabccba(由abccba+abccba组成)

abcbaabcba(有abcba+abcba组成)

abccbabccba(由abccba+abccba组成组成,但是中间的1是共用的)

a(一个单独字符也算)

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long int ULL;
const int N = 200010;

int P = 131;
ULL p[N], h[N], ed[N];
int ask1(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}
int ask2(int l, int r)
{
    return ed[l] - ed[r + 1] * p[r - l + 1];
}
int main()
{
    int ans = 0;
    char str[N];
    cin >> str + 1;
    int n = strlen(str + 1);
    p[0] = 1;
    for (int i = 1; i <= n; i++)
    {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
    for (int i = n; i >= 0; i--)
    {
        ed[i] = ed[i +1] * P + str[i];
    }
    for (int i = 1; i <= n; i++)
    {
        if (i % 2 == 1)
        {
            int x = (i + 1) / 2;
            if (ask1(1, x) == ask1(x, i) && ask1(1, x) == ask2(1, x))
                ans++;
        }
        else
        {
            int x = i / 2;
            if (ask1(1, x) == ask1(x + 1, i) && ask1(1, x) == ask2(1, x))
                ans++;
        }
    }
    cout << ans ;
}

回文串匹配算法（马拉车算法）

#include <bits/stdc++.h> ///求解最长回文串，对p[i]/2求和即可得回文串个数
using namespace std;
typedef long long ll;
char a[500500]={0};
int l[500500]={0};
int r[500500]={0};
string str="$#";
vector<int>p;
void manacher(char *c)
{
    int max_id=0,id=0;
    for(int i=1;c[i];i++)
        str+=c[i],str+="#";
    p.push_back(1);
    for(int i=1;i<(int)str.size();i++)
    {
        if(max_id>i)
            p.push_back(min(max_id-i,p[2*id-i]));  
        else
            p.push_back(1);
        while(i+p[i]<(int)str.size()&&str[i+p[i]]==str[i-p[i]])
            p[i]++;
        if(i+p[i]>max_id){
            max_id=i+p[i],id=i;
        }
    }
}
int main()
{
    scanf("%s",a+1);
    manacher(a);
    int now=0,n=str.size(),ans=0;
    for(int i=0;i<n;i++)
        ans=max(ans,p[i]-1);
    printf("%d",ans);
}

字典树

从一组数据中选取两个数求最大异或值。

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[1005000]={0};
int tree[5000500][3]={0};
int tot=1;///必须从1开始
int in(int x)
{
    int p=1;
    for(int i=30;i>=0;i--)
    {
        int k=x>>i&1;
        if(tree[p][k]==0)
            tree[p][k]=++tot;
        p=tree[p][k];
    }
}
int out(int x)
{
    int p=1,ans=0;
    for(int i=30;i>=0;i--)
    {
        int k=x>>i&1;
        if(tree[p][!k])
        {
            ans=ans*2+!k;
            p=tree[p][!k];
        }
        else
        {
            ans=ans*2+k;
            p=tree[p][k];
        }
    }
    return ans;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    int max1=0;
    for(int i=1;i<=n;i++)
    {
       in(a[i]);
       int num=out(a[i]);
       max1=max(max1,num^a[i]);
    }
    cout<<max1<<endl;
    return 0;
}

文法分析

参考链接：

https://blog.csdn.net/qq_40736036/article/details/89110584

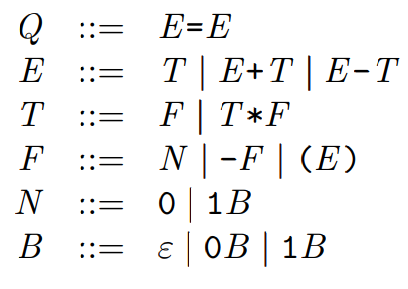
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const ll mod = 10000;
char c[5000500] = {0};
struct grammer
{
    pair<char *, ll> Q(char *p)
    {
        pair<char *, ll> ans1 = E(p);

        if (ans1.first == NULL)
            return {NULL, 0};
        ans1.second %= mod;
        return ans1;
    }
    pair<char *, ll> E(char *p)
    {
        pair<char *, ll> ans1 = T(p);
        if (ans1.first == NULL)
            return {NULL, 0};
        while (*ans1.first == '+' || *ans1.first == '-')
        {
            pair<char *, ll> ans2 = T(ans1.first + 1);
            if (ans2.first == NULL)
                return {NULL, 0};
            if (*ans1.first == '+')
                ans1.second += ans2.second;
            else if (*ans1.first == '-')
                ans1.second -= ans2.second;
            ans1.second = (ans1.second % mod + mod) % mod;
            ans1.first = ans2.first;
        }
        return ans1;
    }
    pair<char *, ll> T(char *p)
    {
        pair<char *, ll> ans1 = F(p);
        if (ans1.first == NULL)
            return {NULL, 0};
        while (*ans1.first == '*')
        {
            pair<char *, ll> ans2 = F(ans1.first + 1);

            if (ans2.first == NULL)
                return {NULL, 0};
            ans1.second *= ans2.second;
            ans1.second %= mod;
            ans1.first = ans2.first;
        }
        return ans1;
    }
    pair<char *, ll> F(char *p)
    {
        if (*p >= '0' || *p <= '9')
        {
            return N(p);
        }
        else if (*p == '-')
        {
            pair<char *, ll> ans1 = F(p + 1);
            if (ans1.first == NULL)
                return {NULL, 0};
            return {ans1.first, (-ans1.second % mod + mod) % mod};
        }
        else if (*p == '(')
        {
            pair<char *, ll> ans1 = E(p + 1);
            if (ans1.first == NULL)
                return {NULL, 0};
            if (*ans1.first == ')')
                return {ans1.first + 1, ans1.second % mod};
            else
                return {NULL, 0};
        }
        else
        {
            return {NULL, 0};
        }
    }
    pair<char *, ll> N(char *p)
    {
        if (*p == '0')
        {
            // if (*(p + 1) >= '0' || *(p + 1) <= '9')
            //     return {NULL, 0};
            // else
            return {p + 1, 0};
        }
        else if (*p >= '1' && *p <= '9')
        {
            pair<char *, ll> ans1 = B(p);
            if (ans1.first == NULL)
            {
                return {NULL, 0};
            }
            return {ans1.first, ans1.second % mod};
        }
        else
        {
            return {NULL, 0};
        }
    }
    pair<char *, ll> B(char *p)
    {
        ll sum = 0;
        while (*p >= '0' && *p <= '9')
        {
            sum = sum * 10 + *p - '0';
            p++;
            sum %= mod;
        }
        return {p, sum % mod};
    }
} Grammer;
int main()
{
    scanf("%s", c + 1);
    ll ans = (Grammer.Q(c + 1).second % mod + mod) % mod;
    printf("%lld\n", ans);
}

AC自动机

参考链接：

https://www.cnblogs.com/nullzx/p/7499397.html

https://zhuanlan.zhihu.com/p/80325757

https://oi-wiki.org/string/ac-automaton/

AC自动机模板：

给定 $n$ 个模式串 $s_i$ 和一个文本串 $t$，求有多少个不同的模式串在文本串里出现过。

两个模式串不同当且仅当他们**编号**不同。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 6;
int n;

namespace AC
{
    int tr[N][26], tot;
    int e[N], fail[N];
    void insert(char *s)
    {
        int u = 0;
        for (int i = 1; s[i]; i++)
        {
            if (!tr[u][s[i] - 'a'])
                tr[u][s[i] - 'a'] = ++tot; //如果没有则插入新节点
            u = tr[u][s[i] - 'a'];         //搜索下一个节点
        }
        e[u]++; //尾为节点 u 的串的个数
    }
    queue<int> q;
    void build()
    {
        for (int i = 0; i < 26; i++)
            if (tr[0][i])
                q.push(tr[0][i]);
        while (q.size())
        {
            int u = q.front();
            q.pop();
            for (int i = 0; i < 26; i++)
            {
                if (tr[u][i])
                {
                    fail[tr[u][i]] =
                        tr[fail[u]][i]; // fail数组：同一字符可以匹配的其他位置
                    q.push(tr[u][i]);
                }
                else
                    tr[u][i] = tr[fail[u]][i];
            }
        }
    }
    int query(char *t)
    {
        int u = 0, res = 0;
        for (int i = 1; t[i]; i++)
        {
            u = tr[u][t[i] - 'a']; // 转移
            for (int j = u; j && e[j] != -1; j = fail[j])
            {
                res += e[j], e[j] = -1;
            }
        }
        return res;
    }
} // namespace AC

char s[N];
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%s", s + 1), AC::insert(s);
    scanf("%s", s + 1);
    AC::build();
    printf("%d", AC::query(s));
    return 0;
}

正则表达式

参考于：https://www.cnblogs.com/luowentao/p/10332311.html

1.规则
{n}匹配确定的n次 
{n,}至少匹配n次(注:请不要擅自加空格上去) 
{n,m}最少n次,最多m次. 
*匹配前面的子表达式0次或多次 = {0,} 
+匹配前面的子表达式1次或多次 = {1,} 
?匹配前面的子表达式1次或两次 = {1,2} 
()表示一个整体 
[]表示一位 
{}表示匹配多少次 
.匹配除换行符之外的任意字符 
\w匹配单字字符(a-z,A-Z,0-9以及下划线) 
\W匹配非单字字符 
\s匹配空白字符(空格,制表符,换行符) 
\S匹配非空白字符 
\d匹配数字字符 
\D匹配非数字字符 
^指示从行的开始位置开始匹配(还有声明不在字符集指定范围内) 
$指示从行的结束位置开始匹配 
\b匹配单词的开始或结束位置

2.速记理解
. [ ] ^ $四个字符是所有语言都支持的正则表达式，所以这四个是基础的正则表达式。正则难理解因为里面有一个等价的概念，这个概念大大增加了理解难度，让很多初学者看起来会懵，如果把等价都恢复成原始写法，自己书写正则就超级简单了，就像说话一样去写你的正则了：

等价：
    等价是等同于的意思，表示同样的功能，用不同符号来书写。

?,*,+,\d,\w 都是等价字符
　　?等价于匹配长度{0,1}
　　*等价于匹配长度{0,} 
　　+等价于匹配长度{1,}
　　\d等价于[0-9]
   \D等价于[^0-9]
   \w等价于[A-Za-z_0-9]
   \W等价于[^A-Za-z_0-9]。

常用运算符与表达式：
　　^ 开始
　　() 域段
　　[] 包含,默认是一个字符长度
　　[^] 不包含,默认是一个字符长度
　　{n,m} 匹配长度 
　　. 任何单个字符(\. 字符点)
　　| 或
　　\ 转义
　　$ 结尾
　　[A-Z] 26个大写字母
　　[a-z] 26个小写字母
　　[0-9] 0至9数字
   [A-Za-z0-9] 26个大写字母、26个小写字母和0至9数字

, 分割
　　分割语法：
　　[A,H,T,W] 包含A或H或T或W字母
　　[a,h,t,w] 包含a或h或t或w字母
　　[0,3,6,8] 包含0或3或6或8数字


语法与释义：
　　基础语法 "^([]{})([]{})([]{})$"
　　正则字符串 = "开始（[包含内容]{长度}）（[包含内容]{长度}）（[包含内容]{长度}）结束" 
　　
　　?,*,+,\d,\w 这些都是简写的,完全可以用[]和{}代替，在(?:)(?=)(?!)(?<=)(?<!)(?i)(*?)(+?)这种特殊组合情况下除外。
　　初学者可以忽略?,*,+,\d,\w一些简写标示符，学会了基础使用再按表自己去等价替换
　　
　　实例：
　　字符串；tel:086-0666-88810009999
　　原始正则："^tel:[0-9]{1,3}-[0][0-9]{2,3}-[0-9]{8,11}$" 
　　速记理解：开始 "tel:普通文本"[0-9数字]{1至3位}"-普通文本"[0数字][0-9数字]{2至3位}"-普通文本"[0-9数字]{8至11位} 结束"
　　等价简写后正则写法："^tel:\d{1,3}-[0]\d{2,3}-\d{8,11}$" ，简写语法不是所有语言都支持。

3.代码实例
3.1 示例一
// 定义一个正则表达式 , 4~23 位数字和字母的组合
regex repPattern("[0-9a-zA-Z]{4,23}",regex_constants::extended);
// 声明匹配结果变量
match_results<string::const_iterator> rerResult;
// 定义待匹配的字符串
string strValue = "123abc";
// 进行匹配
bool bValid = regex_match(strValue, rerResult, repPattern);
if (bValid)
{
    // 匹配成功
}

3.2 示例二
#include <bits/stdc++.h>
using namespace std;
regex r("(\\d|[1-9]\\d|1\\d{2}|2[0-4]\\d|25[0-5])\\.(\\d|[1-9]\\d|1\\d{2}|2[0-4]\\d|25[0-5])\\.(\\d|[1-9]\\d|1\\d{2}|2[0-4]\\d|25[0-5])\\.(\\d|[1-9]\\d|1\\d{2}|2[0-4]\\d|25[0-5]):(\\d|[1-9]\\d{1,3}|[1-5]\\d{4}|6[0-4]\\d{3}|65[0-4]\\d{2}|655[0-2]\\d|6553[0-5])");
int main()
{
    String a;
    cin >> a;
    if (!regex_match(b, r))
        puts("No");
    else
        puts("Yes");
}


4.常用的正则表达式
4.1 检验数字的表达式
数字 : ^[0-9]*$
n 位的数字 : ^\d{n}$
至少 n 位的数字 : ^\d{n,}$
m-n 位的数字 : ^\d{m,n}$
零和非零开头的数字 : ^(0|[1-9][0-9]*)$
非零开头的最多带两位小数的数字 : ^([1-9][0-9]*)+(.[0-9]{1,2})?$
带 1~2 位小数的正数或负数 : ^(\-)?\d+(\.\d{1,2})?$
正数 , 负数 , 和小数 : ^(\-|\+)?\d+(\.\d+)?$
有两位小数的正实数 : ^[0-9]+(.[0-9]{2})?$
有 1~3 位小数的正实数 : ^[0-9]+(.[0-9]{1,3})?$
非零的正整数 : ^[1-9]\d*$ 或 ^([1-9][0-9]*){1,3}$ 或 ^\+?[1-9][0-9]*$
非零的负整数 : ^\-[1-9][]0-9″*$ 或 ^-[1-9]\d*$
非负整数 : ^\d+$ 或 ^[1-9]\d*|0$
非正整数 : ^-[1-9]\d*|0$ 或 ^((-\d+)|(0+))$
非负浮点数 : ^\d+(\.\d+)?$ 或 ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0$
非正浮点数 : ^((-\d+(\.\d+)?)|(0+(\.0+)?))$ 或 ^(-([1-9]\d*\.\d*|0\.\d*[1-9]\d*))|0?\.0+|0$
正浮点数 : ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*$ 或 ^(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*))$
负浮点数 : ^-([1-9]\d*\.\d*|0\.\d*[1-9]\d*)$ 或 ^(-(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*)))$
浮点数 : ^(-?\d+)(\.\d+)?$ 或 ^-?([1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0)$

4.2 检验字符的表达式
汉字 : ^[\u4e00-\u9fa5]{0,}$
英文和数字 : ^[A-Za-z0-9]+$ 或 ^[A-Za-z0-9]{4,40}$
长度为 3~20 的所有字符 : ^.{3,20}$
由 26 个英文字母组成的字符串 : ^[A-Za-z]+$
由 26 个大写英文字母组成的字符串 : ^[A-Z]+$
由 26 个小写英文字母组成的字符串 : ^[a-z]+$
由数字和 26 个英文字母组成的字符串 : ^[A-Za-z0-9]+$
由数字 , 26 个英文字母或者下划线组成的字符串 : ^\w+$ 或 ^\w{3,20}$
中文 , 英文 , 数字包括下划线 : ^[\u4E00-\u9FA5A-Za-z0-9_]+$
中文 , 英文 , 数字但不包括下划线等符号 : ^[\u4E00-\u9FA5A-Za-z0-9]+$ 或 ^[\u4E00-\u9FA5A-Za-z0-9]{2,20}$
可以输入含有^%&',;=?$\"等字符 : [^%&',;=?$\x22]+
禁止输入含有 ~ 的字符 : [^~\x22]+

4.3 特殊需求表达式
Email 地址 : ^\w+([-+.]\w+)*@\w+([-.]\w+)*\.\w+([-.]\w+)*$
域名 : [a-zA-Z0-9][-a-zA-Z0-9]{0,62}(/.[a-zA-Z0-9][-a-zA-Z0-9]{0,62})+/.?
InternetURL : [a-zA-z]+://[^\s]* 或 ^http://([\w-]+\.)+[\w-]+(/[\w-./?%&=]*)?$
手机号码 : ^(13[0-9]|14[5|7]|15[0|1|2|3|5|6|7|8|9]|18[0|1|2|3|5|6|7|8|9])\d{8}$
电话号码("XXX-XXXXXXX" , "XXXX-XXXXXXXX" , "XXX-XXXXXXX" , "XXX-XXXXXXXX" , "XXXXXXX"和"XXXXXXXX) : ^($$\d{3,4}-)|\d{3.4}-)?\d{7,8}$
国内电话号码 (0511-4405222 , 021-87888822) : \d{3}-\d{8}|\d{4}-\d{7}
身份证号 (15 位 , 18 位数字) : ^\d{15}|\d{18}$
短身份证号码 (数字 , 字母 x 结尾) : ^([0-9]){7,18}(x|X)?$ 或 ^\d{8,18}|[0-9x]{8,18}|[0-9X]{8,18}?$
帐号是否合法(字母开头，允许 5~16 字节，允许字母数字下划线) : ^[a-zA-Z][a-zA-Z0-9_]{4,15}$
密码 (以字母开头，长度在 6~18 之间，只能包含字母 , 数字和下划线) : ^[a-zA-Z]\w{5,17}$
强密码 (必须包含大小写字母和数字的组合，不能使用特殊字符，长度在 8~10 之间) : ^(?=.*\d)(?=.*[a-z])(?=.*[A-Z]).{8,10}$
日期格式 : ^\d{4}-\d{1,2}-\d{1,2}
一年的 12 个月(01～09和1～12) : ^(0?[1-9]|1[0-2])$
一个月的 31 天(01～09和1～31) : ^((0?[1-9])|((1|2)[0-9])|30|31)$

数论

整数分块

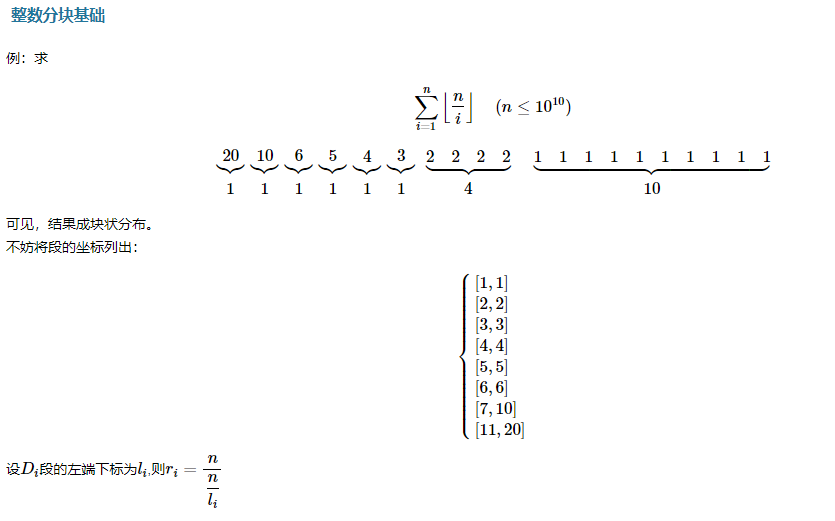
代码实现：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    ll n, ans = 0;
    scanf("%lld", &n);
    for (ll l = 1, r; l <= n; l = r + 1)
    {
        r = n / (n / l);
        ans += (r - l + 1) * (n / l);
    }
    printf("%lld\n", ans);
}

线性筛求质因数的个数

///参照于：
//https://www.luogu.com.cn/blog/SuuTTT/solution%2Dp1029
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
const ll maxn=1e7+5;
ll low_prime[10050000]={0};
ll prime[700500]={0};
ll cnt=0;
int main()
{
    for(ll i=2;i<=maxn;i++)
    {
        if(low_prime[i]==0)
        {
            low_prime[i]=i;
            prime[++cnt]=i;
        }
        for(ll j=1;j<=cnt&&prime[j]*i<=maxn;j++)
        {
            low_prime[prime[j]*i]=prime[j];
            if(i%prime[j]==0)
                break;
        }
    }
    ll t;
    scanf("%lld",&t);
    while(t--)
    {
        ll n,flag=0;
        scanf("%lld",&n);
        for(ll i=1;i<=n;i++)
        {
            ll m,sum=0;
            scanf("%lld",&m);
            while(m>1)
            {
                m/=low_prime[m];
                sum++;
            }
            flag^=sum; ///sum即为质因数的个数
        }
        if(!flag)
            puts("Bob");
        else
            puts("Alice");
    }
}

欧拉函数模板

#include <bits/stdc++.h>
using namespace std;
int is_prime[100500]={0};
vector<int>prime;
int oula_table[100500]={0};
void init(int n)  ///打素数表
{
    for(int i=2;i<=n;i++)
    {
        if(!is_prime[i])
            prime.push_back(i);
        for (int j = 0; j <=prime.size() && i*prime[j] <= n; j++) {
            is_prime[i*prime[j]] = 1;
            if (i % prime[j] == 0)
                break;
        }
    }
}
int oula1(int n) ///根据素数表求解欧拉函数
{
    int ans=n;
    for(int i=0;prime[i]*prime[i]<=n;i++)
    {
        if(n%prime[i]==0)
            ans=ans-ans/prime[i];
        while(n%prime[i]==0)
            n/=prime[i];
    }
    return ans;
}
int oula2(int n)  ///分解质因数法求解欧拉函数
{
    int m=n;
    int ans=n;
    for(int i=2;i<=sqrt(n);i++)
    {
        if(m%i==0)
            ans=ans-ans/i;
        while(m%i==0)
            m/=i;
    }
    if(m!=1)
        ans=ans-ans/m;
    return ans;
}
void get_oula_table(int n) ///欧拉打表
{
    for(int i=1;i<=n;i++)
        oula_table[i]=0;
    oula_table[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!oula_table[i]) ///说明i是质数
        {
            for(int j=i;j<=n;j+=i) //去找i的倍数
            {
                if(!oula_table[j])
                    oula_table[j]=j;
                oula_table[j]=oula_table[j]/i*(i-1);
            }
        }
    }
}
int main()
{
    int n;
    cin>>n;
    init(n);
    cout<<"找素数求解欧拉函数值为"<<oula1(n)<<endl;
    cout<<"分解质因数法求解欧拉函数值为"<<oula2(n)<<endl;
    get_oula_table(n);
    cout<<"打表法求解欧拉函数值为";
    for(int i=1;i<=n;i++)
        cout<<oula_table[i]<<' ';
}

逆序对

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int a[2005000]= {0};
int b[2005000]= {0};
long long int merge_sort(long long int l,long long int r)
{
    if (l >= r)
        return 0;
    long long int mid = (l + r) >> 1, res = 0;
    res += merge_sort(l, mid);
    res += merge_sort(mid + 1, r);
    long long int i = l, j = mid + 1, cnt = 0;
    while (i <= mid && j <= r)
        if (a[i] <= a[j])
            b[cnt++] = a[i++];
        else
        {
            res += mid - i + 1;
            b[cnt++] = a[j++];
        }
    while (i <= mid)
        b[cnt++] = a[i++];
    while (j <= r)
        b[cnt++] = a[j++];
    for (long long int i = l, j = 0; j < cnt; ++i, ++j)
        a[i] = b[j];
    return res;
}
int main()
{
    int n;
    cin>>n;
    for(long long int i=0;i<n; i++)
    {
        cin>>a[i];
    }
    long long int sum=merge_sort(0,n-1);
    cout<<sum<<endl;
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
ll a[100500]={0};
ll c[100500]={0};
ll maxn=10050,k,ans=0;
ll lowbit(ll x)
{
    return x&(-x);
}
ll add(ll k,ll x)
{
    for(ll i=k;i<=maxn;i+=lowbit(i))
        c[i]+=x;
}
ll getsum(ll k)
{
    ll ans=0;
    for(ll i=k;i>=1;i-=lowbit(i))
        ans+=c[i];
    return ans;
}
int main()
{
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++)
    {
        scanf("%lld",&k);
        add(k,1);
        ans+=i-getsum(k);
    }
    printf("%d\n",ans);
}

二维前缀和

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5010;
int g[maxn][maxn];
int main(void)
{
    int N,R;
    cin >> N >> R;
    int n = R, m = R;
    for(int i = 0,x,y,w;i < N;++i)
    {
        cin >> x >> y >> w;
        x++,y++;
        n = max(n,x);
        m = max(m,y);
        g[x][y] += w;
    }
    for(int i = 1; i <= n; i++)
        for(int j = 1;j <= m; j++)
            g[i][j] += g[i-1][j] + g[i][j-1] - g[i-1][j-1];
    int ans = 0;
    for(int i = R;i <= n;i++)
        for(int j = R;j <= m;j++)
            ans = max(ans,g[i][j]-g[i-R][j]-g[i][j-R]+g[i-R][j-R]);
    cout << ans ;
    return 0;
}

扩展欧几里得定理

1. 求解$a * x + b * y = gcd(a,b) $方程的通解x和y

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e9+7;
ll exgcd(ll a, ll b, ll &x, ll &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ll d = exgcd(b, a%b, x, y);
    ll t = x;
    x = y;
    y = t-(a/b)*y;
    return d;
}
int main()
{
    ll a=3,b=5,x=0,y=0;
    ll g=exgcd(a,b,x,y);
    cout<<"特解为"<<"x="<<x<<",y="<<y<<endl;
    for(int i=1;i<=5;i++)
    {
        x+=b/g;
        y-=a/g;
        cout<<"通解为"<<"x="<<x<<",y="<<y<<endl;
    }
    return 0;
}

1. 求解一般方程$a * x+b * y=c$的通解x和y

将方程转变为：$a * x+b * y=gcd(a, b) * c/gcd(a, b);$

最终即为：$a * x/(c/gcd(a, b))+b * y/(c/gcd(a, b))=gcd(a, b);$

即把结果调整为：$x1=x0 * c/gcd(a, b); y1=y0 * c/gcd(a, b);$

#include<stdio.h>
long long exgcd(long long a, long long b, long long &x, long long &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    long long r=exgcd(b, a%b, x, y), t;
    t=x;
    x=y;
    y=t-(a/b)*y;
    return r;
}
int main()
{
    long long a, b, c, ans, x, y;
    while(scanf("%lld%lld%lld", &a, &b, &c)!=EOF)
    {
        ans=exgcd(a, b, x, y);
        if(c%ans==0)
        {
            x=-x*c/ans;
            y=-y*c/ans;
            printf("%lld %lld\n", x, y);
        }
        else
            printf("-1\n");
    }
    return 0;
}

逆元

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a,q;
ll ksm(ll n,ll k)
{
    ll sum1=1,sum2=n;
    while(k!=0)
    {
        if(k%2==1)
            sum1=sum1*sum2%q;
        sum2=sum2*sum2%q;
        k/=2;
    }
    return sum1;
}
int main()
{
    cout<<"请输入a和q的值"<<endl;
    cin>>a>>q;
    cout<<"a关于模q的逆元为"<<ksm(a,q-2)<<endl;
}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a,ll b,ll& x,ll& y) ///后两个参数为引用
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ll gcd_ans=exgcd(b,a%b,x,y);
    ll tem=x;
    x=y;
    y=tem-a/b*y;
    return gcd_ans;
}
int main()
{
    cout<<"请输入a和q的值"<<endl;
    ll a,q,x=0,y=0;
    cin>>a>>q;
    ll gcd_ans=exgcd(q,a,x,y);
    ll mul=q/gcd_ans;
    y=(y%mul+mul)%mul;
    cout<<"a关于模q的逆元为"<<y<<endl;
}

表达式求值（中缀表达式转后缀表达式）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
stack<char> sc;
stack<ll> sll;
char a[100500] = {0};
inline ll qpow(ll a, ll b)
{
    ll ans = 1;
    while (b)
    {
        if (b & 1)
            ans *= a;
        a *= a, b >>= 1;
    }
    return ans;
}

int cmp1(char a1, char a2)
{
    if (a2 == '(')
        return -1;

    if (a2 == ')')
    {
        if (a1 == '(')
            return 0;
        else if (a1 == '#')
            return 0;
        else
            return 1;
    }
    if (a2 == '+' || a2 == '-')
    {
        if (a1 == '+' || a1 == '-' || a1 == '*' || a1 == '/' || a1 == '^')
            return 1;
        else
            return -1;
    }
    if (a2 == '*' || a2 == '/')
    {
        if (a1 == '*' || a1 == '/' || a1 == '^')
            return 1;
        else
            return -1;
    }
    if (a2 == '^')
    {
        if (a1 == '^')
            return 1;
        else
            return -1;
    }
    if (a2 == '#')
    {
        if (a1 == '#')
            return 0;
        else if (a1 == '(' || a1 == ')')
            return 0;
        else
            return 1;
    }
    return 0;
}
int main()
{
    scanf("%s", a + 1);
    a[strlen(a + 1) + 1] = '#';
    ll tem = 0, tem2, tem1;
    sll.push(0);
    sc.push('#');
    for (int i = 1; a[i]; i++)
    {
        if (a[i] <= '9' && a[i] >= '0')
        {
            tem = tem * 10 + a[i] - '0';
            if (a[i + 1] < '0' || a[i + 1] > '9')
                sll.push(tem), tem = 0;
        }
        else
        {
            while (!sc.empty())
            {
                ll tem_cmp = cmp1(sc.top(), a[i]);
                if (tem_cmp == 1)
                {
                    tem2 = sll.top();
                    sll.pop();

                    tem1 = sll.top();
                    sll.pop();

                    if (sc.top() == '+')
                        sll.push(tem1 + tem2);
                    else if (sc.top() == '-')
                        sll.push(tem1 - tem2);
                    else if (sc.top() == '*')
                        sll.push(tem1 * tem2);
                    else if (sc.top() == '/')
                        sll.push(tem1 / tem2);
                    else if (sc.top() == '^')
                        sll.push((ll)qpow(tem1, tem2));
                    sc.pop();
                }
                else if (tem_cmp == 0)
                {
                    if (a[i] != ')' || (a[i] == ')' && sc.size() > 1))
                        sc.pop();
                    break;
                }
                else if (tem_cmp == -1)
                {
                    sc.push(a[i]);
                    break;
                }
            }
        }
    }
    cout << sll.top() << endl;
}

组合数学

参考博客：https://blog.csdn.net/Luoxiaobaia/article/details/107593528

1.球同，盒不同，不能空（隔板法）

一共有n-1个空隙(总共n+1个空隙，不能空要去掉头尾=n-1) ，要插m-1个板，答案为 $C_{n-1}^{m-1}$​

2.球同，盒不同，能空

如果给每个盒子一个球，就可以把问题转化为不能空的情况了,就相当于n+m个小球放入m个盒子且不能空，答案就是 $C_{n+m-1}^{m-1}$

3.球不同，盒同，不能空（dp问题）

dp[n][m]代表n个小球放入m个不同的盒子且不能空的方法

当 i >= 0 时，dp[i][i]=1 (i个小球放入i个盒子，就只能1个盒子放1个)

当 i > 0 时,dp[i][0]=0(都没有盒子了，肯定无解)

dp[i][j] = j * dp[i-1][j] + dp[i-1][j-1]

(第i个球可以放在已经有的j个盒子的一个，有j种方法,也就是j*dp[i-1][j],

也可以是放入一个新的盒子,就是dp[i-1][j-1]) 所以答案如下：

4.球不同，盒同，可以空（第二类斯特林数）

那就是3的情况(球不同，盒同，不允许为空)用1个盒子+用2个盒子+…+m个盒子

5.球不同，盒不同，不能空

那就是3的情况(球不同，盒同，不允许为空)对盒子进行全排列 答案就是 m!*dp[n][m] (dp[n][m]是第二类斯特林数)

6.球不同，盒不同，可以空

每一个小球都有m种方法，且相互独立，答案就是$m^n$

7.球同，盒同，可以空（dp问题）

dp[i][j]代表球同，盒同，可以空的放法 当 i>=j 时，dp[i][j] = dp[i][j-1]+dp[i-j][j]

( 我们可以在所有的盒子上放一个球dp[i-j][j]，也可以不选择这种操作，但是以后都不对其中一个盒子进行操作了，那就是dp[i][j-1] )

当 i<j 时，dp[i][i] (多余的盒子都没有什么卵用了)

当 j=1 时，1(只有一个盒子了就只能放在那个盒子了，只有一种放法)

当 i=1 时，1(只有一个球了，放哪个盒子都一样，只有一种放法)

当 i=0 时 1(没有球了，也是1种方法)

答案是

8.球同，盒同，不能空

那就是7的情况(球同，盒同，可以空)每个盒子先放一个保证不空

所以答案是 dp[n-m][m] (n>=m) 0 (n<m)

其中dp是情况7的dp

附情况7的代码：

#include <iostream>
int main() {
    const int N = 11;
    int dp[N][N] = {}, t, n, m;
    for(int i=0; i<N; ++i)
        for(int j=1; j<N; ++j) {
            if(i<=1 || j==1)  dp[i][j] = 1;
            else if(i<j)  dp[i][j] = dp[i][i];
            else  dp[i][j] = dp[i][j-1] + dp[i-j][j];
        }
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d", &n, &m);
        printf("%d\n", dp[n][m]);
    }
    return 0;
}

卡特兰数

参照博客：https://zhuanlan.zhihu.com/p/97619085

卡特兰数（Catalan number）是 组合数学 中一个常出现在各种 计数问题 中的 数列。

数列的前几项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862，...

卡特兰数公式：

电影购票问题

电影票一张 50 coin，且售票厅没有 coin。m 个人各自持有 50 coin，n 个人各自持有 100 coin。

则有多少种排队方式，可以让每个人都买到电影票。

思路

持有 50 coin 的人每次购票时不需要找零，并且可以帮助后面持有 100 coin 的人找零；而对于持有 100 coin 的人每次购票时需要找零，但 100 coin 对后面的找零没有任何作用。

因此，相当于每个持有 100 coin 的人都需要和一个持有 50 coin 的人进行匹配。我们将持有 50 coin 的标记为 +1，持有 100 coin 的标记为 -1，此时又回到了进出栈问题。

不同的是，m 并一定等于 n，且排队序列是一种排列，需要考虑先后顺序，例如各自持有 50 coin 的甲和乙的前后关系会造成两种不同的排队序列。所以，将会有

第二项为什么是 ，其实很简单，我们每次把第一个前缀小于0 的前缀取反后，会造成 +1 多了一个而 -1 少了一个。这里 +1 有 m 个，-1 有 n 个，取反后 +1 变成m + 1个，-1 变成n - 1个，总和不变。

const int C_maxn = 1e4 + 10;
ll CatalanNum[C_maxn];
ll inv[C_maxn];
inline void Catalan_Mod(int N, LL mod)
{
    inv[1] = 1;
    for (int i = 2; i <= N + 1; i++) ///线性预处理 1 ~ N 关于 mod 的逆元
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;

    CatalanNum[0] = CatalanNum[1] = 1;

    for (int i = 2; i <= N; i++)
        CatalanNum[i] = CatalanNum[i - 1] * (4 * i - 2) % mod * inv[i + 1] % mod;
}

积性函数

积性函数是指对于任意互质的整数a和b有性质f(ab)=f(a)f(b)的数论函数

常用积性函数有：

φ(n) －欧拉函数

μ(n) －莫比乌斯函数，关于非平方数的质因子数目

gcd(n,k) －最大公因子，当k固定的情况

d(n) －n的正因子数目

σ(n) －n的所有正因子之和

莫比乌斯反演

参考于

https://zhuanlan.zhihu.com/p/45744228

函数定义

辅助定理

对于任意正整数 ，恒有

其次，莫比乌斯反演和欧拉函数的关系：

$\sum_{d|n}\frac{\mu[d]}{d}=\frac{\varphi(n)}{n}$

莫比乌斯反演定理

和 是定义在正整数集合上的两个函数，若

则

反之亦然.

证明：

莫比乌斯反演实际上是容斥。

常见反演

1、

所以莫比乌斯函数本身也可以反演。

2、

线性预处理

求解区间 和区间 上互质的数的个数。

代码

void get_mu(int n)
{
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
 }

FFT和NNT模板

参考链接：

https://www.acwing.com/file_system/file/content/whole/index/content/1563813/

https://blog.csdn.net/hzf0701/article/details/119428159

https://blog.csdn.net/zz_1215/article/details/40430041

https://www.luogu.com.cn/problem/P3803

NTT 快速数论变换取模多项式模板

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const ll G = 3;
ll n, m, L, R[6005000] = {0};
ll a[6005000] = {0}, b[6005000] = {0}, inv[6005000] = {0};
ll qpow(ll a, ll b)
{
    ll ans1 = 1, ans2 = a;
    while (b != 0)
    {
        if (b & 1)
            ans1 = ans1 * ans2 % mod;
        ans2 = ans2 * ans2 % mod;
        b /= 2;
    }
    return ans1 % mod;
}

void NTT(ll *a, ll f)
{
    for (ll i = 0; i < n; i++)
    {
        if (i < R[i])
            swap(a[i], a[R[i]]);
    }
    for (ll i = 1; i < n; i <<= 1)
    {
        ll gn = qpow(G, (mod - 1) / (i << 1));
        for (ll j = 0; j < n; j += (i << 1))
        {
            ll g = 1;
            for (ll k = 0; k < i; k++, g = g * gn % mod)
            {
                ll x = a[j + k], y = g * a[j + k + i] % mod;
                a[j + k] = (x + y) % mod;
                a[j + k + i] = (x - y + mod) % mod;
            }
        }
    }
    if (f == 1)
        return;
    ll inv = qpow(n, mod - 2);
    reverse(a + 1, a + n);
    for (ll i = 0; i < n; i++)
        a[i] = 1ll * a[i] * inv % mod;
}
void solve(ll *A, ll *B)
{
    m = n + m;
    for (n = 1; n <= m; n <<= 1)
        L++;
    for (int i = 0; i < n; i++)
        R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
    NTT(A, 1);
    NTT(B, 1);
    for (int i = 0; i < n; i++)
        A[i] = (A[i] % mod * B[i] % mod + mod) % mod;
    NTT(A, -1);
}
int main()
{
    scanf("%lld%lld", &n, &m);
    for (ll i = 0; i <= n; i++)
        scanf("%lld", &a[i]);
    for (ll i = 0; i <= m; i++)
        scanf("%lld", &b[i]);
    solve(a, b);
    for (ll i = 0; i <= m; i++)
        printf("%lld ", a[i]);
    return 0;
}

FFT快速傅里叶变换模板

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> pii;
typedef long long ll;
const int N = 6e6 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const double PI = acos(-1.0); //圆周率PI。

struct Complex
{
    double x, y; //复数，x代表实部，y代表虚部。
    Complex(double _x = 0, double _y = 0)
    {
        x = _x, y = _y;
    }
} a[N], b[N];                 //多项式a和b，相乘。
int n, m, l, r[N], limit = 1; //n为a的次数,m为b的次数。limit即为最大限制。2^n次方，而l为二进制的位数
//运算符重载。
Complex operator+(Complex a, Complex b)
{
    return Complex(a.x + b.x, a.y + b.y);
}
Complex operator-(Complex a, Complex b)
{
    return Complex(a.x - b.x, a.y - b.y);
}
//复数相乘，则模长相乘，幅度相加。
Complex operator*(Complex a, Complex b)
{
    return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);
}
void fft(Complex *A, int type)
{
    for (int i = 0; i < limit; ++i)
    {
        if (i < r[i])
            swap(A[i], A[r[i]]);
        //求出要迭代的区间。小于r[i]时才交换，防止同一个元素交换两次，回到原来的位置。
    }
    //从底层往上合并。
    for (int mid = 1; mid < limit; mid <<= 1)
    {
        //待合并区间长度的一半，最开始是两个长度为1的序列合并,mid = 1;
        Complex Wn(cos(PI / mid), type * sin(PI / mid)); //单位根。
        for (int len = mid << 1, j = 0; j < limit; j += len)
        {
            //len是区间的长度，j是当前的位置，也就是合并到了哪一位。
            Complex w(1, 0); //幂，一直乘，得到平方，三次方。
            for (int k = 0; k < mid; ++k, w = w * Wn)
            {
                //枚举左半部分。蝴蝶变换得到右半部分的答案。w为wn * k
                Complex x = A[j + k], y = w * A[j + mid + k]; //左半部分和右半部分。
                A[j + k] = x + y;                             //左边加。
                A[j + mid + k] = x - y;                       //右边减。
            }
        }
    }
    if (type == 1)
        return;
    for (int i = 0; i <= limit; ++i)
    {
        a[i].x /= limit;
        //最后需要除以limit也就是补成了2的整数幂。将点值转换为系数。
    }
}
void solve()
{
    while (limit <= n + m)
    {
        limit <<= 1, l++;
    }
    //初始化r数组。
    for (int i = 0; i < limit; ++i)
    {
        r[i] = (r[i >> 1] >> 1) | ((i & 1) << (l - 1));
    }
    fft(a, 1); //将a的系数转化为点值表示，
    fft(b, 1); //将b的系数转化为点值表示。
    for (int i = 0; i <= limit; ++i)
    {
        //对应项相乘，得到点值表示的解。
        a[i] = a[i] * b[i];
    }
    fft(a, -1);
    for (int i = 0; i <= n + m; ++i)
    {
        //取出来除2，加上0.5四舍五入。
        printf("%d ", (int)(a[i].x + 0.5));
    }
    printf("\n");
}
int main()
{
    scanf("%d%d", &n, &m);
    //读入多项式的每一项。
    for (int i = 0; i <= n; ++i)
    {
        scanf("%lf", &a[i].x);
    }
  ·  for (int i = 0; i <= m; ++i)
    {
        scanf("%lf", &b[i].x);
    }
    solve();
    return 0;
}

Meissel-Lehmer 算法

是一种能在亚线性时间复杂度内求出 1∼n内质数个数的一种算法。

时间复杂度$O(n^{\frac{2}{3}})$

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
//通过知道前面的 n^1/3 的质数可以推断后面n^2/3的质数所以可以适当减小
const int N  = 9e3;
const int M  = 2;         //为了减小内存可以不过是质数
const int PM = 2 * 3 * 5; //为了减小内存可以不过要按质数减小如去掉17
ll n;
bool np[N];
int prime[N], pi[N];
int phi[PM + 1][M + 1], sz[M + 1];

int getprime() {
    int cnt = 0;
    np[0] = np[1] = true;
    pi[0] = pi[1] = 0;
    for (int i = 2; i < N; ++i) {
        if (!np[i]) prime[++cnt] = i;
        pi[i] = cnt;
        for (int j = 1; j <= cnt && i * prime[j] < N; ++j) {
            np[i * prime[j]] = true;
            if (i % prime[j] == 0) break;
        }
    }
    return cnt;
}

void init() {
    getprime();
    sz[0] = 1;
    for (int i = 0; i <= PM; ++i) phi[i][0] = i;
    for (int i = 1; i <= M; ++i) {
        sz[i] = prime[i] * sz[i - 1];
        for (int j = 1; j <= PM; ++j) phi[j][i] = phi[j][i - 1] - phi[j / prime[i]][i - 1];
    }
}

int sqrt2(ll x) {
    ll r = (ll)sqrt(x - 0.1);
    while (r * r <= x) ++r;
    return int(r - 1);
}

int sqrt3(ll x) {
    ll r = (ll)cbrt(x - 0.1);
    while (r * r * r <= x) ++r;
    return int(r - 1);
}

ll getphi(ll x, int s) {
    if (s == 0) return x;
    if (s <= M) return phi[x % sz[s]][s] + (x / sz[s]) * phi[sz[s]][s];
    if (x <= prime[s] * prime[s]) return pi[x] - s + 1;
    if (x <= prime[s] * prime[s] * prime[s] && x < N) {
        int s2x = pi[sqrt2(x)];
        ll ans  = pi[x] - (s2x + s - 2) * (s2x - s + 1) / 2;
        for (int i = s + 1; i <= s2x; ++i) ans += pi[x / prime[i]];
        return ans;
    }
    return getphi(x, s - 1) - getphi(x / prime[s], s - 1);
}

ll getpi(ll x) {
    if (x < N) return pi[x];
    ll ans = getphi(x, pi[sqrt3(x)]) + pi[sqrt3(x)] - 1;
    for (int i = pi[sqrt3(x)] + 1, ed = pi[sqrt2(x)]; i <= ed; ++i) ans -= getpi(x / prime[i]) - i + 1;
    return ans;
}

ll lehmer_pi(ll x) { //小于等于n的素数有多少个
    if (x < N) return pi[x];
    int a  = (int)lehmer_pi(sqrt2(sqrt2(x)));
    int b  = (int)lehmer_pi(sqrt2(x));
    int c  = (int)lehmer_pi(sqrt3(x));
    ll sum = getphi(x, a) + (ll)(b + a - 2) * (b - a + 1) / 2;
    for (int i = a + 1; i <= b; i++) {
        ll w = x / prime[i];
        sum -= lehmer_pi(w);
        if (i > c) continue;
        ll lim = lehmer_pi(sqrt2(w));
        for (int j = i; j <= lim; j++) sum -= lehmer_pi(w / prime[j]) - (j - 1);
    }
    return sum;
}

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    init();
    while (cin >> n && n) cout << lehmer_pi(n) << "\n";
    return 0;
}

Miller Rabin素数判定算法

// C++ Version
bool millerRabin(int n) {
  if (n < 3 || n % 2 == 0) return n == 2;
  int a = n - 1, b = 0;
  while (a % 2 == 0) a /= 2, ++b;
  // test_time 为测试次数,建议设为不小于 8
  // 的整数以保证正确率,但也不宜过大,否则会影响效率
  for (int i = 1, j; i <= test_time; ++i) {
    int x = rand() % (n - 2) + 2, v = quickPow(x, a, n);
    if (v == 1) continue;
    for (j = 0; j < b; ++j) {
      if (v == n - 1) break;
      v = (long long)v * v % n;
    }
    if (j >= b) return 0;
  }
  return 1;
}

动态规划

最长上升子序列

如果你需要移动一样东西，显然接触或者使用磁场电场之类的可以解决。但是有没有办法进行超越距离的随心所欲的移动？ 对于物体或者文字进行超距离移动一直是人类的梦想，有一天这个难题终于被我们的大牛解决了！他现在需要的就是整理数列。数列就是所谓的写在纸上或者在电脑品目上的数列... 整理数列需要一个叫做swap的操作，swap操作就是指大牛通过超距离的控制把数列中的某一位直接插入某两位的中间或者数列的开始或者终止的操作。这个操作的关键在于超距离控制，显然这种事情不能干太多次，不但降RP，而且很耗体力。你的任务就是从初始状态到目标状态所需要做swap的最少次数。

输入 三行，第一行一个整数 n（n<600000） 第二行，n 个整数（1-n），表示初始数列。 第三行，n 个整数（1-n），表示目标数列。 保证整数不重复。

输出 一行 表示最少swap次数。 样例输入 10 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 样例输出 9

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<iostream>
#include<cstdio>
#include <bits/stdc++.h>
using namespace std;
const int inf=0x7fffffff;
int b[1005001],mp[1005001],c[1005001];
int main()
{
    int n,x;
    cin>>n;
    for(int i=1; i<=n; i++)
        scanf("%d",&x),mp[x]=i;
    for(int i=1; i<=n; i++)
        scanf("%d",&b[i]),c[i]=inf;
    int len=0;
    c[0]=0;
    for(int i=1; i<=n; i++)
    {
        int l=0,r=len,mid;
        if(mp[b[i]]>c[len])
            c[++len]=mp[b[i]];
        else
        {
            while(l<r)
            {
                mid=(l+r)/2;
                if(c[mid]>mp[b[i]])
                    r=mid;
                else
                    l=mid+1;
            }
            c[l]=min(mp[b[i]],c[l]);
        }
    }
    cout<<n-len<<endl;
    return 0;
}

最长公共子序列

for(int i = 1; i <= strlen(a); i ++)
        for(int j = 1; j <= strlen(b); j ++)
            if(a[i] == b[j])
                dp[i][j] = dp[i-1][j-1] + 1;
            else
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);

状压DP

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef long long ll;

const int inf=0x3f3f3f3f;
int n,m;

struct node{
     int cost,num;
}nd[100005];

int f[1005][(1<<12)+5];//1左移12位再加5

int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int b;
        scanf("%d%d",&nd[i].cost,&b);
        int t=0;
        for(int j=1;j<=b;j++)
        {
              int temp;
              scanf("%d",&temp);
              t|=(1<<(temp-1));///1本来就在第一个位，所以要到第temp位，只需要向左移动temp-1位
        }
        nd[i].num=t;
    }
    memset(f,inf,sizeof(f));
    f[0][0]=0;///很重要
    for(int i=1;i<=m;i++)
    {
        for(int j=0;j<(1<<n);j++)///n个锁
        {
            int kk=j|nd[i].num;///对应每个锁选不选
            f[i][kk]=min(f[i][kk],f[i-1][j]+nd[i].cost);
            f[i][j]=min(f[i][j],f[i-1][j]);///
        }
    }
    if(f[m][(1<<n)-1]!=inf)///1向左移动12，相当于1000000000000，然而12个位置都为1，即(111111111111)=(1000000000000)-1
        printf("%d\n",f[m][(1<<n)-1]);
    else printf("-1");
    return 0;
}

斜率DP

优化$ Dp[i]=min(Dp[i]，Dp[j]+(h[j]-h[i])^2 +m)(m为常数)$

题目链接：

Frog 3-ICPC

Frog 3-Atcoder

参考链接：

https://www.cnblogs.com/orzzz/p/7885971.html

https://blog.csdn.net/mengxiang000000/article/details/78113980

https://blog.csdn.net/bllsll/article/details/78267029

公式推导：

我们假设在求解$dp[i]$时，存在$j,k(j>k)$使得从$j$转移比从$k$转移更优，那么需要满足条件：

$dp[j]+(S[i+1]−S[j])^2+M<dp[k]+(S[i+1]−S[k])^2+M$

展开上式

$dp[j]+S[i+1]^2−2S[i+1]S[j]+S[j]^2+M<dp[k]+S[i+1]^2−2S[i+1]S[k]+S[k]^2+M$

移项并消去再合并同类项得

$dp[j]−dp[k]+S[j]^2−S[k]2<2S[i+1] (S[j]−S[k]) $

把S[j]−S[k]S[j]−S[k]除过去，得到

$\frac{dp[j]−dp[k]+S[j]^2−S[k]^2}{S[j]−S[k]}<2S[i+1]$

我们设$f[x]=dp[x]+S[x]^2$，就化成了

$\frac{f[j]−f[k]}{S[j]−S[k]}<2S[i+1]$

即当$(j>k)$时，若$\frac{f[j]−f[k]}{S[j]−S[k]}<2S[i+1]$，则$j$对更新$dp[i]$比$k$更新$dp[i]$优。---斜率。

当一个数的dp值求完了，它的f值也跟着确定，我们就可以在空间中绘制出点(S[i],f[i])。这个点代表已经求出dp值的一个点。

当我们要求解dp[t]时，如果可用的集合里存在这样三个点，位置关系如图所示：

那么显然

$\frac{f[j]−f[k]}{S[j]−S[k]}>\frac{f[i]−f[j]}{S[i]−S[j]}$

这时候他们和2S[t+1]2S[t+1]的关系有3种：

·$\frac{f[j]−f[k]}{S[j]−S[k]}>\frac{f[i]−f[j]}{S[i]−S[j]}>2S[t+1]$

那么j比i优，k比j优。

·$\frac{f[j]−f[k]}{S[j]−S[k]}>2S[t+1]>\frac{f[i]−f[j]}{S[i]−S[j]}$

那么i比j优，k比j优。

·$2S[t+1]>\frac{f[j]−f[k]}{S[j]−S[k]}>\frac{f[i]−f[j]}{S[i]−S[j]}$

那么i比j优，j比k优。

综上，不管什么样的$S[t+1]$，从j转移都不会是最佳方案。那么用一个数据结构维护一个凸包（下凸），每加入一个点就删去一些点，使其维持凸包的形态。最优转移一定在这个凸包中。

那么根据上述，我们可以有两个推论：

1.$G[j，k]<=S[i]$，那么位子k就可以被淘汰。

2.$G[j，k]<=G[i，j]$，那么表示j比k更优，并且i比j更优，那么位子j是可以被淘汰的。

代码：

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll h[200500] = {0};
ll dp[200500] = {0};
deque<ll> que;
double xielv(ll i, ll j)
{
    double ans = (dp[i] + h[i] * h[i] - dp[j] - h[j] * h[j]) * 1.0 / (2 * (h[i] - h[j]));
    return ans;
}
int main()
{
    ll n, m;
    scanf("%lld%lld", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%lld", &h[i]);
    que.push_back(1);
    dp[1] = 0;
    for (int i = 2; i <= n; i++)
    {
        while (que.size() >= 2 && xielv(que[0], que[1]) <= h[i])
            que.pop_front();
        if (que.size())
            dp[i] = dp[que[0]] + (h[i] - h[que[0]]) * (h[i] - h[que[0]]) + m;
        while (que.size() >= 2 && xielv(que[que.size() - 2], que[que.size() - 1]) > xielv(que[que.size() - 1], i))
            que.pop_back();
        que.push_back(i);
    }
    cout << dp[n] << endl;
}

贪心

区间贪心问题

参考链接：https://www.cnblogs.com/dchnzlh/p/10427309.html

区间选取（会场安排问题），给一个大区间l,r然后给你n个区间，最最多多少个区间没有重复部分

例子：

学校的小礼堂每天都会有许多活动，有时间这些活动的计划时间会发生冲突，需要选择出一些活动进行举办。小刘的工作就是安排学校小礼堂的活动，每个时间最多安排一个活动。现在小刘有一些活动计划的时间表，他想尽可能的安排更多的活动，请问他该如何安排。

输入：

第一行是一个整型数m(m<100)表示共有m组测试数据。 每组测试数据的第一行是一个整数n(1<n<10000)表示该测试数据共有n个活动。 随后的n行，每行有两个正整数Bi,Ei(0<=Bi,Ei<10000),分别表示第i个活动的起始与结束时间（Bi<=Ei)

输出：

对于每一组输入，输出最多能够安排的活动数量。

策略：每选一个之后能给后面的留更多的时间（效果：按结束时间排序）

那么第一个时，肯定选此时能选的结束时间最早的，选其他的话给后面留的时间都比前者小，所以咱们选的第一个肯定没错，就是此时能选的结束时间最早的，然后选第二个时，也是选可选时间中结束最早的，这样保证有其最优解，归纳起来激就是，每个根据当前可用时间，选取一个结束时间最早的，做为下一个会场的安排，

#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=10010;
struct Node{
int beg,end;
}node[maxn];
bool cmp(Node a,Node b)
{
    return a.end<b.end;
}
int main()
{
    int t,n,ans;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=0;i<n;++i)//输入区间 并处理
        {
            scanf("%d %d",&node[i].beg,&node[i].end);
            node[i].end++;//将区间变为左闭右开
        }
        sort(node,node+n,cmp);//将区间按右端点排序,右端点小的在前面
        ans=0;
        int pos=0;//初始化
        //pos意为上一个选取的活动结束的位置,若果beg>=pos就可以安排
        for(int i=0;i<n;++i)
        {
            if(node[i].beg>=pos)
            {
                ++ans;
                pos=node[i].end;
            }
        }
        printf("%d\n",ans);
    }
}

区间选点问题,n个闭区间[ai,bi]，让他取尽量少的点，使得每个闭区间内至少有一个点。

输入：

n个闭区间，

输出：

最少用几个点，把每个区间都包含一个点

策略：让这个点出现在一个没有点的区间上，尽可能覆盖多的区间的地方（效果：按结束处排序）

首先为了将最左边的一个区间覆盖，（按结束排序即可）那么第一个点必须在第一个区间上，那么在区间上哪呢？为了让这个点让更多的区间的区间碰到，让这个点最靠右，这样的话能保证这个点覆盖的地方最多，然后一直往后遍历，直到一个区间不在这个点上时，为了让这个区间被覆盖，必须在从这个区间上找一点，（问题变为了前者） 每次一个点可以解决一个区间或者若干个区间，这遍历完所有区间即可

#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=10010;
struct Node{
int beg,end;
}node[maxn];
bool cmp(Node a,Node b)
{
    return a.end<b.end;
}
int main()
{
    int n,ans;
    while(~scanf("%d",&n))
    {
        for(int i=0;i<n;++i)//输入区间 并处理
        {
            scanf("%d %d",&node[i].beg,&node[i].end);
        }
        sort(node,node+n,cmp);//将区间按右端点排序,右端点小的在前面
        ans=0;
        int pos=-1;//pos代表第一个区间选取的点
        for(int i=0;i<n;++i)
        {
            if(node[i].beg>pos)
            {
                pos=node[i].end;
                ++ans;
            }
        }
        printf("%d\n",ans);
    }
}

区间完全覆盖问题

问题描述：给定一个长度为m的区间（全部闭合），再给出n条线段的起点和终点（注意这里是闭区间），求最少使用多少条线段可以将整个区间完全覆盖

将所有区间化作此区间的区间，剪辑一下（没用的区间删除）

策略：在能连接区间左边的情况下，找到向右边扩展最长的位置。（效果：按开头排序，开头一样，右边最长的靠前）

为了连接到这个**需要被覆盖区间的左边**，选一个左端点最靠前的区间，如果左端点相同让右端点大的排在前面

然后向右扫描区间…，如何找下一个需要安置的区间呢，即直到找到与上一个区间没有连接的地方，这时候必须找一个区间来来作为一个连接，因为前面区间都没有断开，所以在前面扫描过的区间找到一个结束处最大的区间作为连接就行，记下这个能扩展到右边的最大位置（其实这个过程是找边的过程）。如果这个最大位置都不能连着，证明这个区间不能被完全覆盖！即不存在解。

#include<stdio.h>
#include<string>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#include<math.h>
using namespace std;
const int maxn=10010;
struct Node{
double beg,end;
}node[maxn];
bool cmp(Node a,Node b)
{
    if(a.beg==b.beg)
        return a.end>b.end;
    return a.beg<b.beg;
}
int main()
{
    int t,n,cnt=0;
    double w,h;
    int ans=0;
    double x,r;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d %lf %lf",&n,&w,&h);
        cnt=0;
        while(n--)
        {
            scanf("%lf %lf",&x,&r);
            if(r<=h/2.0)//过滤掉无效的喷水装置
                continue;
            double ll,rr;//存下该喷水装置区间的范围
            double mid=sqrt(r*r-(h*h/4.0));
            ll=x-mid;
            rr=x+mid;//将喷水装置转化为能覆盖的区间
            ll=max(0.0,ll);
            rr=min((double)w,rr);
            node[cnt].beg=ll;
            node[cnt].end=rr;
            ++cnt;
        }
        /*
        此时转化为一个区间覆盖问题   即在一个长度为w的区间内  选出最少的区间让这个区间覆盖
        */
        node[cnt].beg=(double)w;
        node[cnt].end=(double)w;//加入一个终端区间[w,w]这样遍历到整个区间最后会找出来一个往右边延伸到w的位置的区间，如果没有就没答案
        ++cnt;
        sort(node,node+cnt,cmp);
        double maxpos,nowpos;
        nowpos=0.0;
        maxpos=0.0;
        int flag=1;//
        ans=0;
        for(int i=0;i<cnt;++i)
        {
            if(node[i].beg<=nowpos)//这个区间可以与前面的区间连着
                maxpos=max(maxpos,node[i].end);//更新课扩展的最大区间
            else
            {
                if(maxpos>=node[i].beg)//遇到一个间隔的 需要找一个区间补一下
                {
                    ans++;
                    nowpos=maxpos;
                    --i;
                }
                else//如果不能补
                {
                    flag=0;
                    break;//无解
                }
            }
        }
        if(flag)
            printf("%d\n",ans);
        else
            printf("0\n");
    }
}

计算机图形学

凸包算法

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define PI 3.1415926535
using namespace std;
struct node
{
    int x,y;
};
node vex[1000];//存入的所有的点
node stackk[1000];//凸包中所有的点
int xx,yy;
bool cmp1(node a,node b)//排序找第一个点
{
    if(a.y==b.y)
        return a.x<b.x;
    else
        return a.y<b.y;
}
int cross(node a,node b,node c)//计算叉积
{
    return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
double dis(node a,node b)//计算距离
{
    return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));
}
bool cmp2(node a,node b)//极角排序另一种方法，速度快
{
    if(atan2(a.y-yy,a.x-xx)!=atan2(b.y-yy,b.x-xx))
        return (atan2(a.y-yy,a.x-xx))<(atan2(b.y-yy,b.x-xx));
    return a.x<b.x;
}
bool cmp(node a,node b)//极角排序
{
    int m=cross(vex[0],a,b);
    if(m>0)
        return 1;
    else if(m==0&&dis(vex[0],a)-dis(vex[0],b)<=0)
        return 1;
    else return 0;
    /*if(m==0)
        return dis(vex[0],a)-dis(vex[0],b)<=0?true:false;
    else
        return m>0?true:false;*/
}
int main()
{
    int t,L;
    while(~scanf("%d",&t),t)
    {
        int i;
        for(i=0; i<t; i++)
        {
            scanf("%d%d",&vex[i].x,&vex[i].y);
        }
        if(t==1)
            printf("%.2f\n",0.00);
        else if(t==2)
            printf("%.2f\n",dis(vex[0],vex[1]));
        else
        {
            memset(stackk,0,sizeof(stackk));
            sort(vex,vex+t,cmp1);
            stackk[0]=vex[0];
            xx=stackk[0].x;
            yy=stackk[0].y;
            sort(vex+1,vex+t,cmp2);//cmp2是更快的，cmp更容易理解
            stackk[1]=vex[1];//将凸包中的第两个点存入凸包的结构体中
            int top=1;//最后凸包中拥有点的个数
            for(i=2; i<t; i++)
            {
                while(i>=1&&cross(stackk[top-1],stackk[top],vex[i])<0)   //对使用极角排序的i>=1有时可以不用，但加上总是好的
                    top--;
                stackk[++top]=vex[i];                                    //控制<0或<=0可以控制重点，共线的，具体视题目而定。
            }
            double s=0;
            //for(i=1; i<=top; i++)//输出凸包上的点
            //cout<<stackk[i].x<<" "<<stackk[i].y<<endl;
            for(i=1; i<=top; i++)   //计算凸包的周长
                s+=dis(stackk[i-1],stackk[i]);
            s+=dis(stackk[top],vex[0]);//最后一个点和第一个点之间的距离
            /*s+=2*PI*L;
            int ans=s+0.5;//四舍五入
            printf("%d\n",ans);*/
            printf("%.2lf\n",s);
        }
    }
}

求任意多边形面积

#include <bits/stdc++.h>
using namespace std;
struct Point{
   double x,y;
}p[100500];
int n;
double polygonarea()
{
    int i,j;
    double area = 0;
    for(i = 1;i <= n;++i){
        if(i<n)
            j=i+1;
        else
            j=1;
        area += p[i].x*p[j].y;
        area -= p[i].y*p[j].x;
    }
    area /= 2.0;
    return (area<0?-area:area);
}
int main()
{
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        for(int i=1;i<=n;i++)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        printf("%.1f\n",polygonarea());
    }
}

扫描线算法

线段树+扫描线求正方形颜色反转

输入：

1
5 2  
2 4 1 3
1 5 3 5

代表1组测试样例，给定5*2的正方形，将2<=x<=4&&1<=y<=3的范围内的小正方形进行黑白反转，求最终黑色正方形的个数，答案为18.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node
{
    int h,a,b,num;
};
int mark[100500]={0};
int sum[100500]={0};
node edge[100500]={0};
bool cmp(node a,node b)
{
    if(a.h==b.h)
        return a.num>b.num;
    else
        return a.h<b.h;
}
int nodeupdate(int root,int l,int r,ll num)
{
    mark[root]^=1;
    sum[root]=r-l+1-sum[root];
}
int pushdown(int root,int l,int r)
{
    if(mark[root]==0)
        return 0;
    int mid=(l+r)/2;
    nodeupdate(2*root,l,mid,mark[root]);
    nodeupdate(2*root+1,mid+1,r,mark[root]);
    mark[root]=0;
}
int update(int root,int l,int r,int L,int R,ll num)
{
    if(l>=L&&r<=R)
    {
        nodeupdate(root,l,r,num);
        return 0;
    }
    pushdown(root,l,r);
    int mid=(l+r)/2;
    if(mid>=L)
        update(root*2,l,mid,L,R,num);
    if(mid<R)
        update(root*2+1,mid+1,r,L,R,num);
    sum[root]=sum[2*root]+sum[2*root+1];
}
int main()
{
    int t,cnt;
    scanf("%d",&t);
    while(t--)
    {
        memset(sum,0,sizeof(sum));
        memset(mark,0,sizeof(mark));
        int n,m,ans=0;
        cnt=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
        {
            int x1,y1,x2,y2;
            scanf("%d%d%d%d",&x1,&x2,&y1,&y2);
            edge[cnt++]=node{y1,x1,x2,1};
            edge[cnt++]=node{y2,x1,x2,-1};
        }
        sort(edge,edge+cnt,cmp);
        for(int i=1,j=0;i<=n;i++)
        {
            while(j<cnt&&edge[j].h<=i&&edge[j].num==1)
            {
                update(1,1,n,edge[j].a,edge[j].b,1);
                j++;
            }
            ans+=sum[1];
            while(j<cnt&&edge[j].h<=i)
            {
                update(1,1,n,edge[j].a,edge[j].b,1);
                j++;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

线段树离散化求面积的并：

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
ll n;
ll s[400500] = {0};
ll len[400500] = {0};
ll x[400500]= {0};
unordered_map<ll,ll>mpx;
void push_up(ll t, ll l, ll r)
{
    if (s[t])
        len[t] = x[r+1] - x[l];
    else if (l == r)
        len[t] = 0;
    else
        len[t] = len[2 * t + 1] + len[2 * t];
}
void update(ll t, ll l, ll r, ll L, ll R, ll add)
{
    if (l <= L && R <= r)
    {
        s[t] += add;
        push_up(t, L, R);
        return;
    }
    ll mid = (L + R) / 2;
    if (l <= mid)
        update(2 * t, l, r, L, mid, add);
    if (mid < r)
        update(2 * t + 1, l, r, mid + 1, R, add);
    push_up(t, L, R);
}
struct node1
{
    ll l,r,h,d;
};
node1 edge[200500]= {0};
bool cmp(node1 a,node1 b)
{
    return a.h<b.h;
}
int main()
{
    scanf("%lld", &n);
    ll cnt=0;
    for (ll i = 1; i <= n; i++)
    {
        ll x1,x2,y1,y2;
        scanf("%lld%lld%lld%lld", &x1, &y1, &x2, &y2);
        x[++cnt]=x1,edge[cnt]= {x1,x2,y1,1};
        x[++cnt]=x2,edge[cnt]= {x1,x2,y2,-1};
    }
    sort(x+1,x+cnt+1);
    sort(edge+1,edge+cnt+1,cmp);
    ll m=unique(x+1,x+cnt+1)-x-1;
    for(int i=1; i<=m; i++)
        mpx[x[i]]=i;
    ll ans = 0;
    for (ll i = 1; i < cnt; i++)
    {
        ll l=mpx[edge[i].l],r=mpx[edge[i].r];
        update(1, l,r-1, 1, m, edge[i].d);
        ans += len[1]*(edge[i+1].h-edge[i].h);
    }
    cout << ans << endl;
}

扫描线维护区间内所有长方形边长长度

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f
using namespace std;
int n;
int lazy[400500] = {0};
int len[400500] = {0};
int x[100500] = {0};
int vis[50050] = {0};
unordered_map<int, int> mpx;
void push_up(int t, int l, int r)
{
    if (l == r)
        len[t] = 0;
    else
        len[t] = len[2 * t + 1] + len[2 * t];
}
void push_down(int t, int l, int r)
{
    if (lazy[t])
    {
        int mid = (l + r) / 2;
        len[2 * t] += lazy[t] * (x[mid + 1] - x[l]);
        len[2 * t + 1] += lazy[t] * (x[r + 1] - x[mid + 1]);
        lazy[2 * t + 1] += lazy[t];
        lazy[2 * t] += lazy[t];
        lazy[t] = 0;
    }
}
int query(int t, int l, int r, int L, int R)
{
    if (l <= L && R <= r)
        return len[t];
    push_down(t, L, R);
    int ans = 0, mid = (L + R) / 2;
    if (l <= mid)
        ans += query(2 * t, l, r, L, mid);
    if (mid < r)
        ans += query(2 * t + 1, l, r, mid + 1, R);
    return ans;
}
void update(int t, int l, int r, int L, int R, int add)
{
    if (l <= L && R <= r)
    {
        lazy[t] += add;
        len[t] += add * (x[r + 1] - x[l]);
        return;
    }
    int mid = (L + R) / 2;
    if (l <= mid)
        update(2 * t, l, r, L, mid, add);
    if (mid < r)
        update(2 * t + 1, l, r, mid + 1, R, add);
    push_up(t, L, R);
}
struct node1
{
    int l, r, h, d, id;
};
node1 edge[100500] = {0};
bool cmp(node1 a, node1 b)
{
    return a.h < b.h;
}
int main()
{
    scanf("%d", &n);
    int cnt = 0;
    for (int i = 1; i <= n; i++)
    {
        int x1, x2, y1, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        x[++cnt] = x1, edge[cnt] = {x1, x2, y1, 1, i};
        x[++cnt] = x2, edge[cnt] = {x1, x2, y2, -1, i};
    }
    sort(x + 1, x + cnt + 1);
    sort(edge + 1, edge + cnt + 1, cmp);
    int m = unique(x + 1, x + cnt + 1) - x - 1;
    for (int i = 1; i <= m; i++)
        mpx[x[i]] = i;
    for (int i = 1; i <= cnt; i++)
    {
        int l = mpx[edge[i].l], r = mpx[edge[i].r];
        if (edge[i].d == 1 && query(1, l, r - 1, 1, m) != 0)
            vis[edge[i].id] = 1;
        if (vis[edge[i].id] == 1)
            continue;
        update(1, l, r - 1, 1, m, edge[i].d);
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans += (!vis[i]);
    cout << ans << endl;
}

博弈论

巴什博弈

只有一堆n个物品，两个人从轮流中取出（1~m）个；最后取光者胜。

若n=k*(m+1) 那么先取者必输。

 int Bash_Game(int n,int m)//是否先手有必赢策略
 {
     if (n%(m+1)!=0) return 1;
     return 0;
 }

尼姆博弈

有若干堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

XOR 判断:

int Nimm_Game(int n)//假设n个数存在数组f[]中,有必胜策略返回1
{
    int flag=0;
    for(int i=1;i<=n;i++)
    flag^=f[i];
    if(flag) return 1;
    return 0;
}

威佐夫博奕

有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

判断是否为奇异局势

设x= k=[a*x]，向上取整

如果a+k=b，则（a，b）为奇异局势，后手胜，反之为先手胜

对应的代码在这里：

int Wythoff_Game(int a,int b)
{
    if(a>b)
        swap(a,b);
    double x=(sqrt(5.0)-1.0)/2.0;
    int k=ceil(1.0*a*x);
    if(a+k==b)
        return 0;//奇异局势，后手胜！
    else
        return 1;//非奇异局势，先手胜！
}

SG函数和NIM博弈

题目题解 题目链接 SG函数详解

#include <bits/stdc++.h>
using namespace std;
bool vis[300]={0};
int sg[110][110]={0};
void init()
{
    for(int i=0;i<=100;i++)
        sg[i][i]=sg[i][0]=sg[0][i]=199;
    for(int i=0;i<=100;i++)
    {
        for(int j=0;j<=100;j++)
        {
            if(i==j||i==0||j==0)
                continue;
            memset(vis,0,sizeof(vis));
            for(int a=0;a<i;a++)
                vis[sg[a][j]]=1;
            for(int b=0;b<j;b++)
                vis[sg[i][b]]=1;
            for(int c=min(i,j);c>=1;c--)
                vis[sg[i-c][j-c]]=1;
            for(int k=0;;k++)
            {
                if(!vis[k])
                {
                    sg[i][j]=k;
                    break;
                }
            }
        }
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    int a,b;
    int nim=0;
    init();
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&a,&b);
        if(a==b)
        {
            printf("Y\n");
            return 0;
        }
        nim^=sg[a][b];
    }
    if(nim!=0)
        printf("Y\n");
    else
        printf("N\n");
}