2021-02-02

A题

题解

签到题目，给定三个数a,b和c，选择一个数x，使得x-2<=a，x-1<=b且x<=c，求3*x-3的最大值。

代码

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int a,b,c;
    cin>>a>>b>>c;
    int min1=min(a+2,min(b+1,c));
    cout<<min1+min1-1+min1-2<<endl;
}

B题

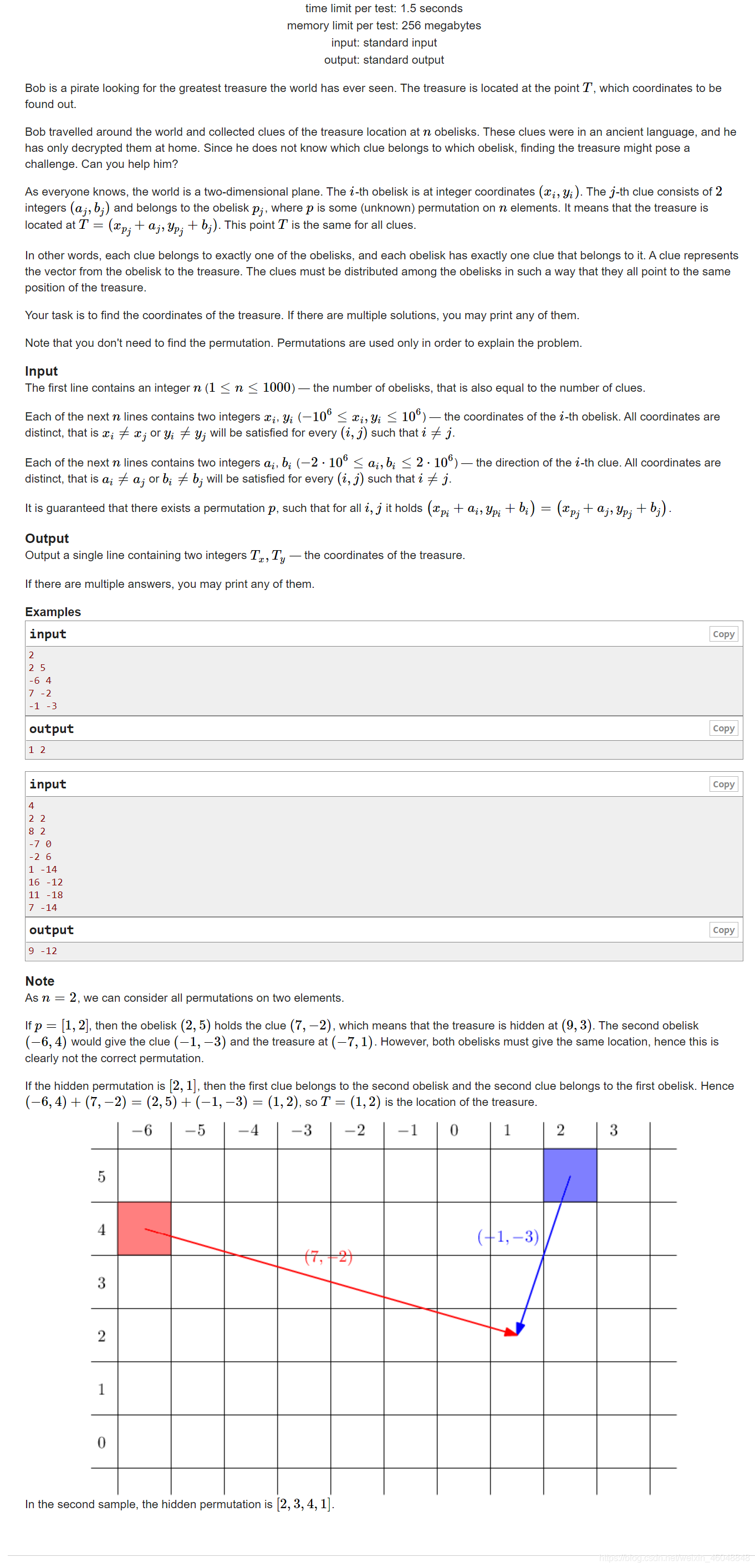
题解

给定2 * n个点，在前n个点中选一个点i，在后n个点中选一个点j，构造一种匹配方式使得任意两点横纵坐标和(xi+xj,yi+yj)均相同。由于xi+xj均相同，可以把这2 * n个点的x坐标进行求和然后平均分配成n份，这样就得到了xi+xj的定值，y坐标同理。（注意开long long）

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
int main()
{
    ll n;
    scanf("%lld",&n);
    ll sum1=0,sum2=0,x,y;
    for(int i=1;i<=2*n;i++)
    {
        scanf("%lld%lld",&x,&y);
        sum1+=x,sum2+=y;
    }
    sum1/=n,sum2/=n;
    cout<<sum1<<' '<<sum2<<endl;
}

C题

题解

该题为打表找规律所做出来的，容易发现这些最小值所对应的k可以和n的因数一一对应，所以只需要枚举n的因数然后求出结果即可。

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
set<ll>s;
ll n;
ll cal(ll x)
{
    ll size1=n/x;
    ll ans=size1+size1*(size1-1)/2*x;
    return ans;
}
int main()
{
    scanf("%lld",&n);
    for(int i=1;i<=sqrt(n);i++)
    {
        if(n%i==0)
        {
            s.insert(cal(i));
            s.insert(cal(n/i));
        }
    }
    set<ll> ::iterator it=s.begin();
    while(it!=s.end())
    {
        cout<<*it<<' ';
        it++;
    }
    cout<<endl;
}

D题

题解

这里以n=4为例

1. 四个数一组，可以组成4! 个答案

2. 第一排当中 每一对数后三个 和 下一对数的第一个 组成一个答案，而第一排中恰有3! 对数，所以答案为(3! - 1)*4

3. 第一排有六对数，可以划分为3组，每组两个，且每组中 上一对数的后两个 和 下一对数的前两个 组成答案，所以答案又应当加上(2! - 1) * 4 * 3

4. 综上答案为4! + (3! - 1) * 4 + (2! - 1) * 4 * 3 =56
5. 同理，5的答案为：5! + (4! - 1) * 5 + (3! - 1) * 5 * 4 + (2! - 1) * 5 * 4 * 3 = 4 *5! - 5 - 5 *4 - 5 *4 *3 = 395
6. 注意特判1 ！！！

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n;
const ll mod=998244353;
int main()
{
    scanf("%lld",&n);
    if(n==1)
    {
        cout<<1<<endl;
        return 0;
    }
    ll ans=1;
    for(ll i=1;i<=n;i++)
    {
        ans=ans*i;
        ans%=mod;
    }
    ans=ans*(n-1);
    ans%=mod;
    ll sum1=1;
    for(ll i=n;i>=3;i--)
    {
        sum1*=i;
        sum1%=mod;
        ans=ans-sum1;
        ans=(ans%mod+mod)%mod;
    }
    ans=(ans%mod+mod)%mod;
    cout<<ans<<endl;
}

I题

题解

图论题目，对于每一个节点，该点到根节点的权值最小值即为子节点权值的最小值，所以先dfs确定-1点的权值s[i]，然后根据得出的权值该点权值s[i]和父节点权值s[i]判断是否符合条件并求和得出答案。

代码

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
vector<ll>v[100500];
ll s[100500]={0};
ll fa[100500]={0};
ll dfs(ll k,ll fa)
{
    ll min1=inf;
    for(int i:v[k])
    {
        if(i!=fa)
        {
            if(dfs(i,k)==-1)
                return -1;
            if(s[i]!=-1)
                min1=min(min1,s[i]);
        }
    }
    if(s[k]==-1)
    {
        if(min1!=inf)
            s[k]=min1;
    }
    else
    {
        if(s[k]>min1)
            return -1;
    }
    return 0;
}
ll ans=0;
ll dfs1(ll k,ll fa,ll sum)
{
    if(s[k]==-1)
        return 0;
    if(s[k]<sum)
        return -1;
    sum=max(sum,s[k]);
    ans=ans+s[k]-s[fa];
    for(int i:v[k])
    {
        if(i!=fa)
        {
            if(dfs1(i,k,sum)==-1)
                return -1;
        }
    }
    return 0;
}
int main()
{
    ll n,m;
    scanf("%lld",&n);
    fa[1]=0;
    for(ll i=2;i<=n;i++)
    {
        scanf("%lld",&m);
        fa[i]=m;
        v[i].push_back(m);
        v[m].push_back(i);
    }
    for(ll i=1;i<=n;i++)
        scanf("%lld",&s[i]);
    s[0]=0;
    if(dfs(1,-1)==-1)
    {
        printf("-1\n");
        return 0;
    }
    if(dfs1(1,0,0)==-1)
    {
        printf("-1\n");
        return 0;
    }
    cout<<ans<<endl;
}