2020-09-11树状数组求最大值
http://icpc.upc.edu.cn/status.php?user_id=2019UPC135&cid=1461
题目描述¶
现在请求你维护一个数列,要求提供以下两种操作:1、查询操作。语法:QL功能:查询当前数列中末尾L个数中的最大的数,并输出这个数的值。限制:L不超过当前数列的长度。2、插入操作。语法:An功能:将n加上t,其中t是最近一次查询操作的答案(如果还未执行过查询操作,则t=0),并将所得结果对一个固定的常数D取模,将所得答案插入到数列的末尾。限制:n是非负整数并且在长整范围内。注意:初始时数列是空的,没有一个数。
输入¶
第一行两个整数,M和D,其中M表示操作的个数(M <= 200,000),D如上文中所述,满足D在longint内。接下来M行,查询操作或者插入操作。
输出¶
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后L个数的最大数。
样例输入¶
样例输出¶
树状数组维护数组求最值 附一张图帮助理解代码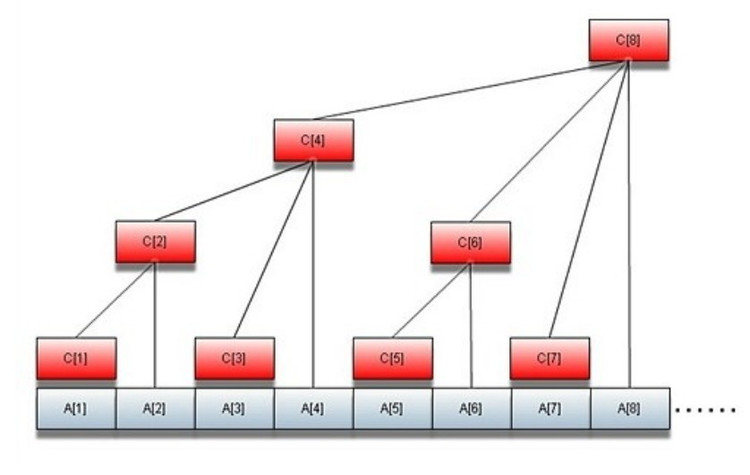
#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
#define inf 0x3f3f3f
using namespace std;
typedef long long ll;
ll c[400500]={0};
ll h[400500]={0};
ll lowbit(ll x)
{
return x&(-x);
}
ll getmax(ll l,ll r)
{
ll max1=h[r];
while(l<=r)
{
max1=max(max1,h[r]);
for(--r;r-l>=lowbit(r);r-=lowbit(r))
max1=max(max1,c[r]);
}
return max1;
}
char s[100];
int main()
{
ll n,d,a,t=0,cnt=0;
scanf("%lld%lld",&n,&d);
while(n--)
{
scanf("%s%lld",s,&a);
if(s[0]=='A')
{
h[++cnt]=(a+t)%d;
c[cnt]=max(getmax(cnt-lowbit(cnt)+1,cnt-1),h[cnt]);
}
else
{
t=getmax(cnt-a+1,cnt);
printf("%d\n",t);
}
}
}
单点修改+区间查询求和¶
题目¶
给定一个数字n,表示数组大小,后有n个数字,表示数组中每个数字的初始值,然后进行m次操作,‘Q’代表查询,查询某一区间所有元素的和,‘C’代表修改,在某一元素上加上值。
输入¶
输出¶
树状数组单点修改+区间求和#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m;
ll h[100500]={0};
ll c[100500]={0};
ll lowbit(ll x)
{
return x&(-x);
}
ll add(ll x,ll a)
{
while(x<=n)
{
c[x]+=a;
x+=lowbit(x);
}
}
ll getsum(ll l)
{
ll sum=0;
while(l>0)
{
sum+=c[l];
l-=lowbit(l);
}
return sum;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&h[i]);
add(h[i],i);
}
char a[100];
ll b,c;
while(m--)
{
scanf("%s%lld%lld",a,&b,&c);
if(a[0]=='Q')
{
printf("%lld\n",getsum(c)-getsum(b-1));
}
else
{
add(b,c);
}
}
return 0;
}
区间修改+区间查询¶
http://icpc.upc.edu.cn/problem.php?cid=1461&pid=13
题目描述¶
You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.
输入¶
The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000. The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000. Each of the next Q lines represents an operation. "C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000. "Q a b" means querying the sum of Aa, Aa+1, ... , Ab.
输出¶
You need to answer all Q commands in order. One answer in a line.
样例输入¶
样例输出¶
提示 The sums may exceed the range of 32-bit integers.#include<bits/stdc++.h>
#define inf 0x3f3f3f
using namespace std;
typedef long long ll;
ll num[400500]={0};
ll sum[400500]={0};
ll lazy[400500]={0};
ll n,m,b,c,d;
ll pushup(ll t)
{
sum[t]=sum[2*t]+sum[2*t+1];
}
ll pushlazy(ll t,ll lz,ll len)
{
sum[t]+=lz*len;
lazy[t]+=lz;
}
ll pushdown(ll l,ll r,ll t)
{
if(lazy[t]!=0)
{
ll mid=(l+r)/2;
pushlazy(2*t,lazy[t],mid-l+1);
pushlazy(2*t+1,lazy[t],r-mid);
lazy[t]=0;
}
}
ll build(ll l,ll r,ll t)
{
lazy[t]=0;
if(l==r)
{
sum[t]=num[l];
return 0;
}
ll mid=(l+r)/2;
build(l,mid,t*2);
build(mid+1,r,2*t+1);
pushup(t);
}
ll add(ll x,ll l,ll r,ll L,ll R,ll t)
{
if(l>=L&&r<=R)
{
lazy[t]+=x;
sum[t]+=(r-l+1)*x;
return 0;
}
pushdown(l,r,t);
ll mid=(l+r)/2;
if(L<=mid)
add(x,l,mid,L,R,2*t);
if(R>mid)
add(x,mid+1,r,L,R,2*t+1);
pushup(t);
}
ll querysum(ll l,ll r,ll L,ll R,ll t)
{
if(l>=L&&r<=R)
return sum[t];
pushdown(l,r,t);
ll mid=(l+r)/2;
ll ans=0;
if(L<=mid)
ans+=querysum(l,mid,L,R,2*t);
if(R>mid)
ans+=querysum(mid+1,r,L,R,2*t+1);
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++)
scanf("%lld",&num[i]);
build(1,n,1);
char a[100]={0};
for(ll i=1;i<=m;i++)
{
scanf("%s",a);
if(a[0]=='C')
{
scanf("%lld%lld%lld",&b,&c,&d);
add(d,1,n,b,c,1);
}
else
{
scanf("%lld%lld",&b,&c);
printf("%lld\n",querysum(1,n,b,c,1));
}
}
}