2020-08-12欧拉函数

http://icpc.upc.edu.cn/problem.php?cid=2539&pid=3

题目描述

Q:KZB 你校本 SA 做完做什么啊？ KZB: 作弊（做 B）啊

有一次，某级某某班的班主任去查了监控，发现 KZB 有人抄作业，就把全班骂了一通。

为了防止这类事情再次发生 Jay 就想出了一道题。

假如整个班为一个n×n的矩阵，而在监控较前面的人会遮住后面的人（详见后面的样例解释）。求监控不会发现的人数（假设监控高度为1）。

Tip: 因为监控在(1,1)的位置，所以会占一个位置。

输入

一个数n。

输出

一个数，即监控不会看到的学生人数。

样例输入

6

样例输出

14

提示

样例解释:当n=6时，坐在(3,5)上的同学会被坐在(2,3)上的同学挡住，以此类推。

可以发现当gcd(x,y)不为1时即照不到，欧拉函数求n数字以内的质因数对有多少即可。

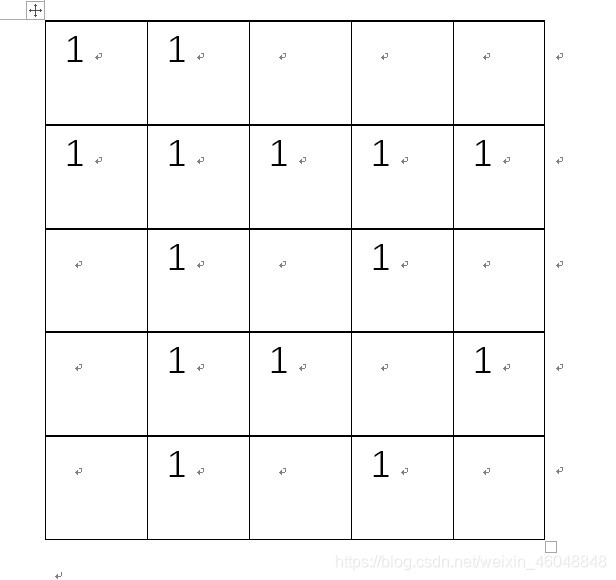图为n为5时的解释，标注为1的是监控能够发现的 欧拉函数简介： https://zhuanlan.zhihu.com/p/42748145

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
ll n, ans, pr[200507], ph[200507], cnt ;
bool vis[200507] ;

int main()  //结合了欧拉筛法
{
    ph[1] = 1 ;
    scanf("%lld", &n );
    if(n==1||n==2)
    {
        cout<<0<<endl;
        return 0;
    }
    for(ll  i = 2 ; i<=n-1; ++ i )  //分解质因数和初始化
    {
        if(!vis[i])
        {
            cnt ++ ;
            pr[cnt] = i ;
            ph[i] = i - 1 ;
        }
        for(ll j = 1 ; j <=cnt&&i*pr[j]<=n-1;++ j )  //欧拉筛法
        {
            vis[ i * pr[j] ] = 1 ;
            if( i % pr[j] == 0 )
            {
                ph[ pr[j] * i ] = ph[i] * pr[j] ;
                break;
            }
            else
                ph [ pr[j] * i] = ph[i] * (pr[j] - 1 );
        }
    }
    for(ll i = 2 ; i <= n-1 ; ++ i )
        ans += ph[i];//累加结果
    ans=ans*2+4;
    ans=n*n-ans;
    cout<<ans<<endl;
    return 0;
}