跳转至

2020-08-05

http://icpc.upc.edu.cn/problem.php?cid=1442&pid=0

题目描述

给定整数N(1≤N≤10^6)，试把阶乘N!分解质因数，按照算术基本定理的形式输出分解结果中的pi和ci即可。

输入

一个整数N。

输出

N! 分解质因数后的结果，共若干行，每行一对pi, ci，表示含有pi^ci项。按照pi从小到大的顺序输出。

样例输入
5
样例输出
2 3
3 1
5 1
提示

5! = 120 = 2^3 * 3 * 5

解析：

欧拉筛法 https://blog.csdn.net/WHZ2018/article/details/81233937 

#pragma GCC optimize(1)
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int pd[1005000]={0};
ll c[1005000]={0};
ll n,k;
int main()
{
    ll cnt=0;
    scanf("%lld",&n);
    pd[0]=pd[1]=1;
    for(ll i=2;i<=n;i++)
    {
        if(!pd[i])
            c[cnt++]=i;
        for(ll j=0;j<cnt&&c[j]*i<=n;j++)
        {
            pd[c[j]*i]=1;
            if(i%c[j]==0)
                break;
        }
    }
    for(ll i=0;i<cnt;i++)
    {
        ll sum=0;
        for(ll j=c[i];j<=n;j=j*c[i])
            sum+=n/j;
        printf("%lld %lld\n",c[i],sum);
    }
    return 0;
}
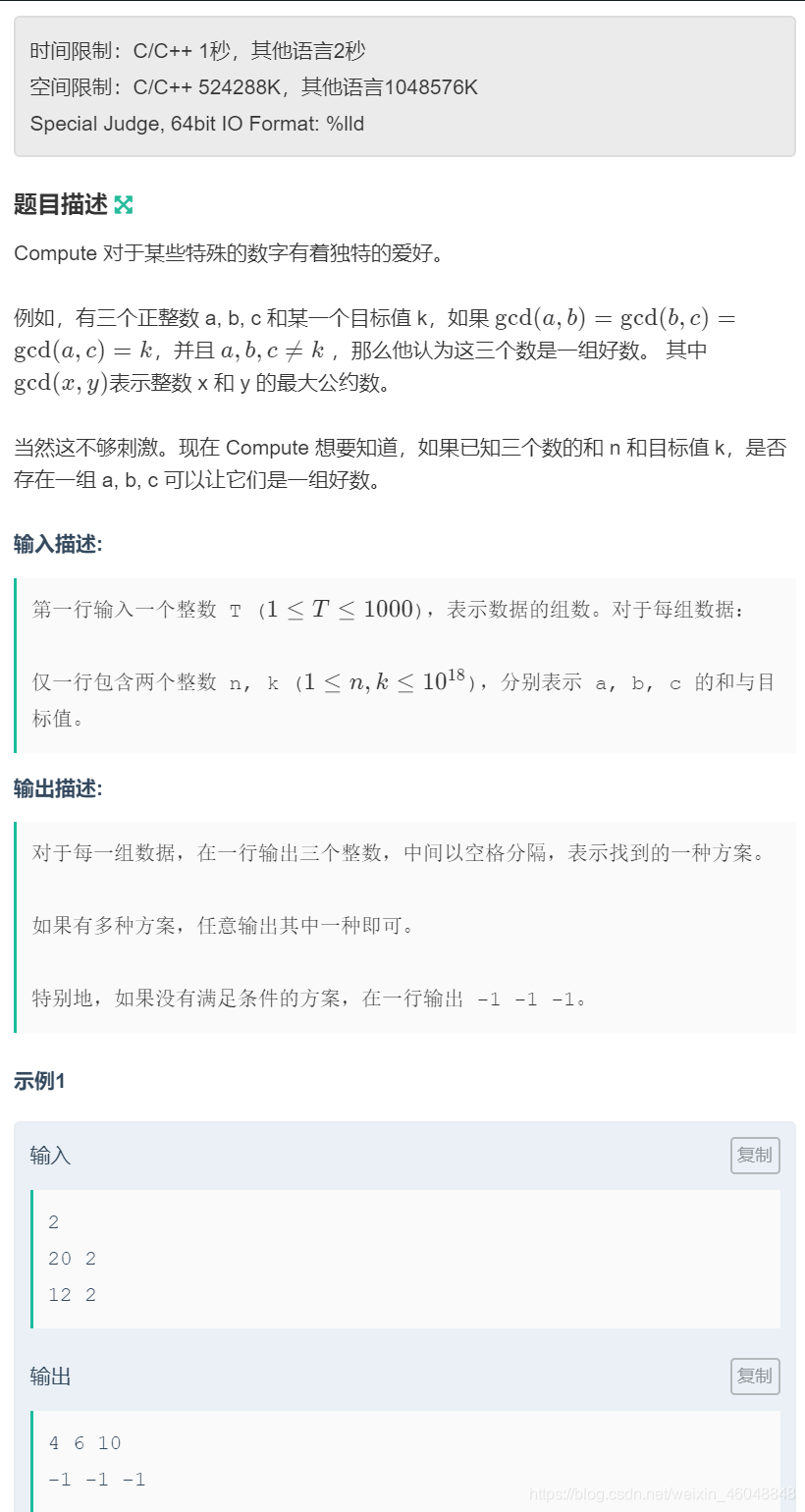在这里插入图片描述 任一大于2的偶数都可写成两个质数之和，分奇偶讨论即可。 
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b)
{
    if(b==0)
        return a;
    else
        return gcd(b,a%b);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n,k;
        scanf("%lld%lld",&n,&k);
        if(n%k!=0)
        {
            puts("-1 -1 -1");continue;
        }
        ll w=n/k,a,b,c;
        int flag=1;
        if(w%2==1)
        {
            a=3,b=2,c=w-a-b;
            while(c>2)
            {
                if(gcd(a,b)==1&&gcd(b,c)==1&&gcd(a,c)==1)
                {
                    flag=0;
                    break;
                }
                b++;c--;
            }
        }
        else
        {
            a=2,b=2,c=w-a-b;
            while(c>2)
            {
                if(gcd(a,b)==1&&gcd(b,c)==1&&gcd(a,c)==1)
                {
                    flag=0;
                    break;
                }
                b++;c--;
            }
        }
        if(flag)
            puts("-1 -1 -1");
        else
            printf("%lld %lld %lld\n",a*k,b*k,c*k);
    }
    return 0;
}

题目

https://ac.nowcoder.com/acm/contest/6871/E

代码

方法1：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
map<ll,ll>w;
char a[2000]= {0};
ll b[3000]= {0};
ll two()
{
    for(ll i=1; i<=8; i++)
    {
        ll w1;
        if(a[i]>='0'&&a[i]<='9')
        {
            w1=a[i]-'0';
        }
        else if(a[i]=='A')
        {
            w1=10;
        }
        else if(a[i]=='B')
        {
            w1=11;
        }
        else if(a[i]=='C')
        {
            w1=12;
        }
        else if(a[i]=='D')
        {
            w1=13;
        }
        else if(a[i]=='E')
        {
            w1=14;
        }
        else if(a[i]=='F')
        {
            w1=15;
        }
        for(ll j=i*4; j>(i-1)*4; j--)
        {
            b[j]=w1%2;
            w1=w1/2;
        }
    }
}
ll six()
{
    ll sum=0;
    for(ll i=1; i<=8; i++)
    {
        sum=0;
        for(ll j=4*(i-1)+1;j<=4*i;j++)
            sum=sum*2+b[j];
        if(sum<=9&&sum>=0)
            printf("%d",sum);
        else if(sum==10)
            printf("A");
        else if(sum==11)
            printf("B");
        else if(sum==12)
            printf("C");
        else if(sum==13)
            printf("D");
        else if(sum==14)
            printf("E");
        else if(sum==15)
            printf("F");
    }
    printf("\n");
}
ll n,m,p,k,summ=1,q,sum1,o;
int main()
{
    scanf("%lld%lld%lld",&n,&m,&p);
    for(ll i=0; i<(1<<(m-p)); i++)
    {
        scanf("%lld",&k);
        w[k]=i;
    }
    scanf("%lld",&q);
    for(ll i=1; i<=q; i++)
    {
        scanf("%s",a+1);
        two();
        sum1=0;
        for(ll i=1; i<=32-p; i++)
            sum1=sum1*2+b[i];
        if(w.find(sum1)==w.end())
        {
            puts("interrupt!");
        }
        else
        {
            o=w[sum1];
            for(ll i=32-p; i>=1; i--)
            {
                b[i]=o%2;
                o=o/2;
            }
            six();
        }
    }
    return 0;
}
方法2：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
map<ll,ll>w;
int main()
{
    ll n,m,p;
    scanf("%lld%lld%lld",&n,&m,&p);
    for (ll i=0;i<1<<(m-p);i++)
    {
        ll pos;
        scanf("%lld",&pos);
        w[pos]=i;
    }
    ll q;
    scanf("%lld",&q);
    while(q--)
    {
        ll tmp;
        scanf("%llX",&tmp);
        printf("%lld\n",tmp);
        ll t1=tmp/(1<<p),t2=tmp%(1<<p);
        if (w.find(t1)==w.end())
        {
            printf("interrupt!\n");
        }
        else
        {
            printf("%08llX\n",w[t1]*(1<<p)+t2);
        }
    }
    return 0;
}