组队训练赛（四）

组队训练赛（四）

题目1

题目链接

智乃酱的前缀和与差分

题目描述

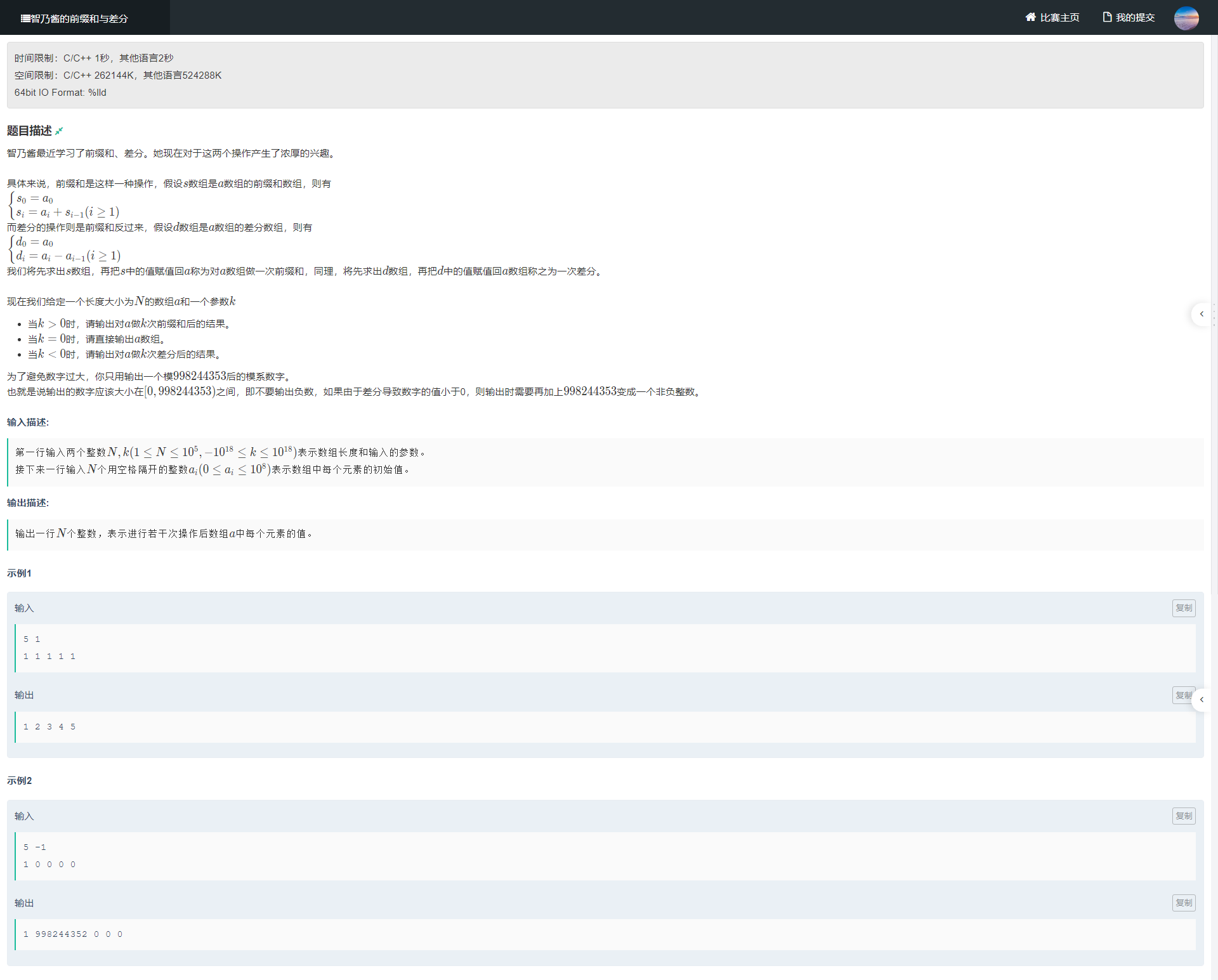
样例输入

10 2 11
1000 1000 1000 100000 1000 1000 10000 10000 10000 100000
1 10 0 100
1 10 1 1 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10 10
1 10

样例输出

1101
1102
1103
100104
1105
1106
10107
10108
10109
100110
236055

题解

由于模数大于序列长度，所以对负数的差分可以转化为取模后的前缀和。

对序列{$a_0$,0,0,0,0}做前缀可得

序号	0	1	2	3	4
原序列	$a_0$	0	0	0	0
一次前缀和	$a_0$	$a_0$	$a_0$	$a_0$	$a_0$
二次前缀和	$a_0$	2$a_0$	3$a_0$	4$a_0$	5$a_0$
三次前缀和	$a_0$	3$a_0$	6$a_0$	10$a_0$	15$a_0$

则可以得到一个递推式：$b[k][i]=b[k-1][i]+b[k][i-1]$，该公式即为从(0,0)点走到(k,i)点的路径种类数，且通项公式即为：

$b[k][i]=C_{i+k-1}^{i-1}$

因此可以通过组合数递推的方式求出系数。

如果考虑${a_0,a_1,a_2,.....,a_k}$序列，则可得到一下计算：

答案即为${a_0,a_1,a_2,...,a_k}$和${b_0,b_1,b_2,...,b_k}$卷积的结果，根据NTT算法可以在$O(nlogn)$时间复杂度内得出答案。

参考链接：

https://blog.nowcoder.net/n/d1e592fc44b648668bcddc3fe44b7927

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const ll G = 3;
ll n, m, L, R[600500] = {0};
ll a[600500] = {0}, b[600500] = {0}, inv[600500] = {0};
ll qpow(ll a, ll b)
{
    ll ans1 = 1, ans2 = a;
    while (b != 0)
    {
        if (b & 1)
            ans1 = ans1 * ans2 % mod;
        ans2 = ans2 * ans2 % mod;
        b /= 2;
    }
    return ans1 % mod;
}

void NTT(ll *a, ll f)
{
    for (ll i = 0; i < n; i++)
    {
        if (i < R[i])
            swap(a[i], a[R[i]]);
    }
    for (ll i = 1; i < n; i <<= 1)
    {
        ll gn = qpow(G, (mod - 1) / (i << 1));
        for (ll j = 0; j < n; j += (i << 1))
        {
            ll g = 1;
            for (ll k = 0; k < i; k++, g = g * gn % mod)
            {
                ll x = a[j + k], y = g * a[j + k + i] % mod;
                a[j + k] = (x + y) % mod;
                a[j + k + i] = (x - y + mod) % mod;
            }
        }
    }
    if (f == 1)
        return;
    ll inv = qpow(n, mod - 2);
    reverse(a + 1, a + n);
    for (ll i = 0; i < n; i++)
        a[i] = 1ll * a[i] * inv % mod;
}
void solve(ll *A, ll *B)
{
    m = n + m;
    for (n = 1; n <= m; n <<= 1)
        L++;
    for (int i = 0; i < n; i++)
        R[i] = (R[i >> 1] >> 1) | ((i & 1) << (L - 1));
    NTT(A, 1);
    NTT(B, 1);
    for (int i = 0; i < n; i++)
        A[i] = (A[i] % mod * B[i] % mod + mod) % mod;
    NTT(A, -1);
}
int main()
{
    ll k;
    scanf("%lld%lld", &n, &k);
    m = n;
    ll nn = n;
    for (ll i = 0; i < n; i++)
        scanf("%lld", &a[i]);

    inv[1] = 1;
    for (ll i = 2; i < 200500; i++)
        inv[i] = (ll)(mod - mod / i) * inv[mod % i] % mod;

    b[0] = 1;
    ll kk = (k % mod + mod) % mod;
    for (ll i = 1; i < n; i++)
        b[i] = b[i - 1] * (i + kk - 1) % mod * inv[i] % mod;
    solve(a, b);
    for (ll i = 0; i < nn; i++)
        printf("%lld ", a[i]);
    return 0;
}

题目2

题目描述

给定正整数 $n$，求 $1\le x,y\le n$且 $gcd(x,y)$为素数的数对 $(x,y)$ 有多少对。

输入格式

只有一行一个整数，代表$n$。

输出格式

一行一个整数表示答案。

输入

4

输出

4

提示

对于样例，满足条件的 (x,y) 为 (2,2)，(2,4)，(3,3)，(4,2)

数据规模与约定

对于 100% 的数据，保证 $1\le n\le10^7$。

题解

莫比乌斯反演。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
bool is_prime[10050000] = {0};
ll prime[5005000] = {0};
ll mu[10050000] = {0};
ll sum[10050000] = {0};
ll cnt = 0;
void get_mu(ll n)
{
    mu[1] = 1;
    for (ll i = 2; i <= n; i++)
    {
        if (!is_prime[i])
        {
            prime[++cnt] = i;
            mu[i] = -1;
        }
        for (ll j = 1; j <= cnt && prime[j] * i <= n; j++)
        {
            is_prime[prime[j] * i] = 1;
            if (i % prime[j] == 0)
                break;
            else
                mu[i * prime[j]] = -mu[i];
        }
    }
}

int main()
{
    ll n;
    scanf("%lld", &n);
    get_mu(n);
    for (ll i = 1; i <= cnt; i++)
        for (ll j = 1; j * prime[i] <= n; j++)
            sum[j * prime[i]] += mu[j];
    for (int i = 1; i <= n; i++)
        sum[i] += sum[i - 1];
    ll ans = 0;
    for (ll l = 1, r; l <= n; l = r + 1)
    {
        r = n / (n / l);
        ans += (sum[r] - sum[l - 1]) * (n / l) * (n / l);
    }
    printf("%lld\n", ans);
    return 0;
}